红黑树（二）：删除

时间：2018-05-12 22:37:28 阅读：179 评论：0 收藏：0 [点我收藏+]

　　红黑树的删除操作，较之插入更为复杂，因为红黑树也是二叉搜索树，所以红黑树的删除流程跟二叉搜索树一样，先找到要删除的目标节点T，如果T没有子节点，则将T直接删除，如果T有一个子节点，则将此子节点替换到T的位置，然后删除T，否则如果有两个子节点，则在T的子树中寻找后继节点X，然后将X的值覆盖到T结点，然后删除此后继节点X。后继节点有两种，一是在T的左子树中找值最大的节点，此节点最多只有一个左子节点，二是在T的右子树中寻找T的最小值的节点，此节点最多只有一个右子节点，两种后继节点选择其一都可以。将后继节点删除后，不管是删除的目标节点T，还是删除的是后继节点X，最后都有一个节点会顶替被删除节点的位置，设为N，删除后还需要对N进行颜色的修正。

　　这里，我们只需要讨论删除后继节点X的情况，因为直接删除目标节点T时，表示目标节点T没有任何子节点，非常简单，而且已经包含在删除后继节点X的情况中。

　　在深入讨论前，先做一些约定，设待删除节点（后继节点）为X，删除后继节点后，代替后继节点位置的节点是N，X的父节点，也就是现在N节点的父节点为P，N的祖父节点为G，N的叔节点为U，U的左子节点为L_,右子节点为为R，如下图所示：

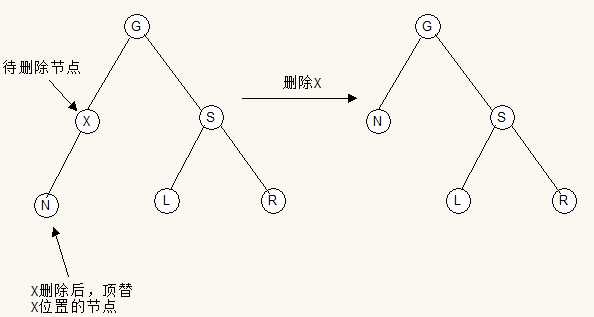
技术分享图片

（以上只作为各节点命名说明，各节点颜色并未标出，N即可为左子节点，也可以是右子节点，看你选择是的哪种后继节点，而且N是可以有一个子节点的，并未画出。）

　　像上一篇红黑树插入操作讨论的一样，红黑树的删除操作有可能破坏红黑树的哪些性质(红黑树的五个性质不熟悉请参考红黑树（一）：插入)呢？性质1，2，3肯定不会被破坏，性质4也不会破坏，那只有可能破坏性质5，操作一个节点当然可能导致某节点的黑高改变了，这时候就需要针对性质5做修正。

　　首先，如果待删除节点X颜色为红点，则直接拿N替换X即可，因为X为红色，所以所有经过X的路径黑高都不受影响，故无需做颜色修正操作，删除完成。

如果X的颜色为黑色，则此时所有经过X的路径的黑高都减小了1，这时候破坏了红黑树的性质5，如果X的子节点N颜色为红色，则直接将N颜色染成黑色，这样顶替X后，经过N的路径黑高仍然保持不变，故无需修正，而当N的颜色为黑色时，则复杂很多，像红黑树的插入操作一样，此处也可以分几种情况来分别讨论。

　　情况一：G为黑色，U，L，R都为黑色

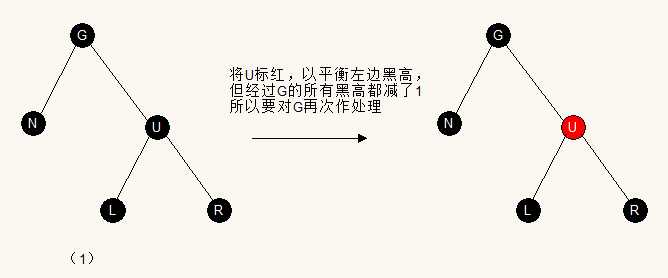
技术分享图片

　　这种情况下，经过N的路径黑高都减小了1，为了将经过N的兄弟U的路径黑高也减小1，直接将U变为黑色，这样在局部维持了红黑树的性质5，但这样一来，经过G的所有路径，其黑高都减小了1，所以这个时候要对G再作处理，也就是向上传递修正。

　　情况二：G为红色，U, L，R都为黑

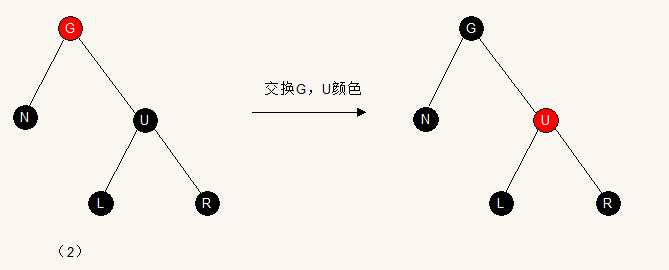
　　技术分享图片

　　这种情况下，直接交换G,U的颜色，即可恢复性质5。

　　情况三：U为红色，G，L，R都为黑

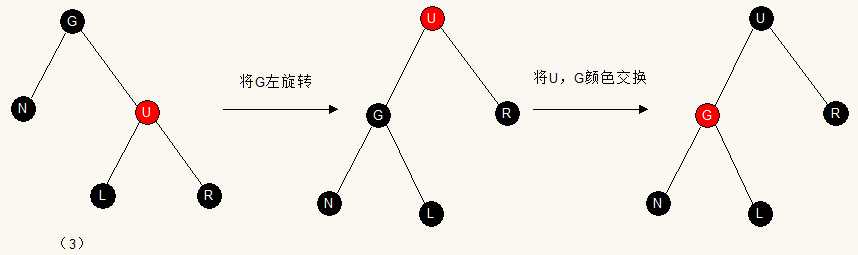
　　技术分享图片

　　这种情况下，经过G->N的路径少了一个黑色节点，此时先将G左旋转，然后交换G，U颜色，这个时候，能过GN的路径多了一个节点N，而其它节点的黑高都没有变化，这个时候，能将G，L颜色互换，以维持经过G->在删除前的黑高吗？没有这么简单，因为我们现在还不知道L节点的子节点是什么颜色，如果是红色，则不能简单交换，以下我们接着讨论，讨论LR的颜色即是接下来的情况四和情况五。

　　情况四：G结点颜色任意，U结点为黑，R节点为红，L节点颜色任一

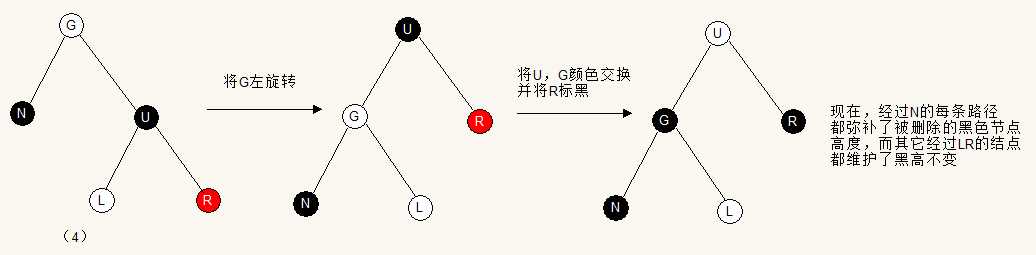
　　技术分享图片

　　这种情况下，将G左旋转，然后将U，G颜色交换，并将R颜色标黑，这个时候，任一节点都维持了删除前的黑高。比如对经过L的路径，删除前是GUL，删除后是UGL，UG颜色前后互换了，但并不影响L此路径黑高。对R的路径，删除前是GUR，删除后是UR，其黑高也没有变。

情况五：G节点颜色任意，U节点为黑，L为红，R为黑（R不讨论红是因为情况四中已包含这种情况）

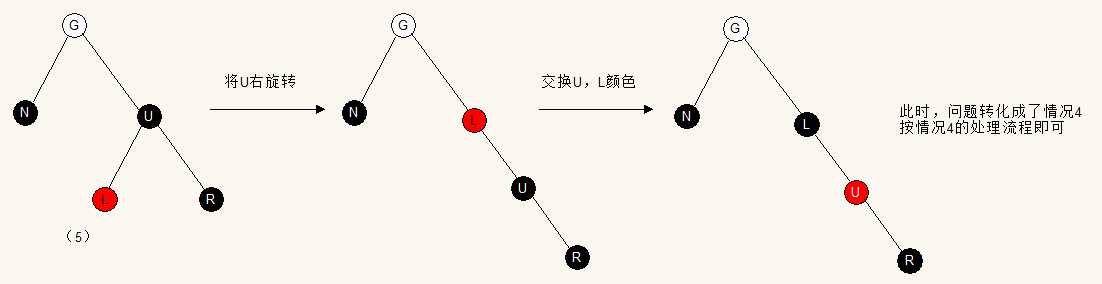
　　技术分享图片

　　这种情况下，将U左旋转，然后交换LU的颜色，这时候可以看出，问题已经转化成情况四了，按情况四的处理流程即可。

情况6：删除后，N是新的根节点，这时候直接将N染成黑色即可。

　　删除总结：

　　　　删除的情况看似多，但各种情况并不是杂乱无章。

　　　　第一种情况全黑，是最简单的情况，但是却要向上传递修正。

　　　　第二，三种情况讨论的是G，U结点分别为红的情况。同时第三种情况引出了情况四和五。

　　　　第四和第五种情况则讨论了一个节点为红和两节点都可能为红的情况。

 1 RBTreeNode* RBTreeDelete(RBTreeNode* pRoot, int nData) {
 2     RBTreeNode* pToDelete = pRoot;
 3 
 4     while (pToDelete != RBTreeNilNodePtr) {
 5         if (nData > pToDelete->nData) {
 6             pToDelete = pToDelete->pRight;
 7         }
 8         else if (nData < pToDelete->nData) {
 9             pToDelete = pToDelete->pLeft;
10         }
11         else
12             break;
13     }
14     if (pToDelete == RBTreeNilNodePtr)
15         return pRoot;
16 
17     if (pToDelete->pLeft != RBTreeNilNodePtr && pToDelete->pRight != RBTreeNilNodePtr) {
18         //RBTreeNode* pMinNode = RBTreeMinimumNode(pToDelete->pRight);
19         RBTreeNode* pMaxNode = RBTreeMaximumNode(pToDelete->pLeft);
20         pToDelete->nData = pMaxNode->nData;
21         pToDelete = pMaxNode;
22     }
23     if (pToDelete->pLeft == RBTreeNilNodePtr || pToDelete->pRight == RBTreeNilNodePtr) {
24         RBTreeNode* pParent = pToDelete->pParent;
25         RBTreeNode* pTemp = (pToDelete->pLeft == RBTreeNilNodePtr) ? pToDelete->pRight : pToDelete->pLeft;
26         bool isRed = pToDelete->isRed;
27 
28         if (pParent != RBTreeNilNodePtr) {
29             if (pParent->pLeft == pToDelete)
30                 pParent->pLeft = pTemp;
31             else
32                 pParent->pRight = pTemp;
33         }
34 
35         if (pTemp != RBTreeNilNodePtr)
36             pTemp->pParent = pParent;
37 
38         if (!isRed) {
39             //删除是的黑色节点
40             if (pToDelete == pRoot) {
41                 pRoot = pTemp;
42             }
43             if (pTemp != RBTreeNilNodePtr) {
44                 if (pTemp->isRed) {
45                     //删除的是黑色节点时，把红色子节点直接变成黑色
46                     pTemp->isRed = RBTreeNodeBlack;
47                 }
48                 else if (pParent != RBTreeNilNodePtr) {
49                     //删除的是一个黑色结点
50                     FixRBTreenodeColor_Delete(&pRoot, pTemp, pTemp->pParent);
51                 }
52             }
53             else if (pParent != RBTreeNilNodePtr) {
54                 FixRBTreenodeColor_Delete(&pRoot, RBTreeNilNodePtr, pParent);
55             }
56         }
57     }
58     delete pToDelete;
59     return pRoot;
60 }

  1 void FixRBTreenodeColor_Delete(RBTreeNode** pRoot, RBTreeNode* pNode, RBTreeNode* pParent) {
  2     if (pParent == RBTreeNilNodePtr && pNode != RBTreeNilNodePtr) {
  3         pNode->isRed = RBTreeNodeBlack;
  4         return;
  5     }
  6     if (pNode->isRed)
  7         return;
  8 
  9     if (pNode == pParent->pLeft) {
 10         RBTreeNode* pBrother = pParent->pRight;
 11         //pBrother不可能为空，否则经过pParent的节点黑高不平衡,pBrotherLeft和pBrotherRight可能是RBTreeNilNodePtr
 12         RBTreeNode* pBrotherLeft = pBrother->pLeft;
 13         RBTreeNode* pBrotherRight = pBrother->pRight;
 14         if (!pBrother->isRed && !pParent->isRed) {
 15             if (!pBrotherLeft->isRed && !pBrotherRight->isRed) {
 16                 //情况1：父节点为黑，兄弟节点及其子节点都为黑
 17                 pBrother->isRed = RBTreeNodeRed;
 18                 FixRBTreenodeColor_Delete(pRoot, pParent, pParent->pParent);
 19             }
 20         }
 21         else if(pBrother->isRed && !pParent->isRed){
 22             //情况3：父节点为黑，兄弟结点为红
 23             //先左旋转父节点
 24             RBTreeNode* pGrandParent = RBTreeLeftRotate(pRoot, pParent);
 25 
 26             pParent = pGrandParent->pLeft;
 27             //再交换颜色 
 28             SwapRBTreeNodeColor(pGrandParent, pParent);
 29             pBrother = pParent->pRight;
 30         }
 31         if (pParent->isRed) {
 32             //pBrother一定是黑
 33             if (!pBrotherLeft->isRed && !pBrotherRight->isRed) {
 34                 //情况2:父节点为红,交换pParent和pBrother的颜色
 35                 SwapRBTreeNodeColor(pParent, pBrother);
 36                 return;
 37             }
 38         }
 39         if (pBrotherLeft->isRed && !pBrotherRight->isRed) {
 40             //情况5：兄弟节点的左子节点为红，此时转化为情况4
 41             //将pBrother右旋转
 42             pBrother = RBTreeRightRotate(pRoot, pBrother);
 43 
 44             pBrotherRight = pBrother->pRight;
 45 
 46             //交换颜色
 47             SwapRBTreeNodeColor(pBrother, pBrotherRight);
 48         }
 49         if (pBrotherRight->isRed) {
 50             //情况4：先左旋转pParent
 51             RBTreeNode* pGrandParent = RBTreeLeftRotate(pRoot, pParent);
 52             pParent = pGrandParent->pLeft;
 53 
 54             //交换颜色
 55             SwapRBTreeNodeColor(pGrandParent, pParent);
 56 
 57             //将pBrotherRight标黑
 58             pBrotherRight->isRed = RBTreeNodeBlack;
 59         }
 60     }
 61     else {
 62         RBTreeNode* pBrother = pParent->pLeft;
 63         //pBrother不可能为空，否则经过pParent的节点黑高不平衡,pBrotherLeft和pBrotherRight可能是RBTreeNilNodePtr
 64         RBTreeNode* pBrotherLeft = pBrother->pLeft;
 65         RBTreeNode* pBrotherRight = pBrother->pRight;
 66 
 67         if (!pBrother->isRed && !pParent->isRed) {
 68             if (!pBrotherLeft->isRed && !pBrotherRight->isRed) {
 69                 //情况1：父节点为黑，兄弟节点及其子节点都为黑
 70                 pBrother->isRed = RBTreeNodeRed;
 71                 FixRBTreenodeColor_Delete(pRoot, pParent, pParent->pParent);
 72             }
 73         }
 74         else if (pBrother->isRed && !pParent->isRed) {
 75             //情况3：父节点为黑，兄弟结点为红
 76             //先左旋转父节点
 77             RBTreeNode* pGrandParent = RBTreeRightRotate(pRoot, pParent);
 78 
 79             pParent = pGrandParent->pRight;
 80             //再交换颜色 
 81             SwapRBTreeNodeColor(pGrandParent, pParent);
 82             pBrother = pParent->pLeft;
 83         }
 84         if (pParent->isRed) {
 85             //pBrother一定是黑
 86             if (!pBrotherLeft->isRed && !pBrotherRight->isRed) {
 87                 //情况2:父节点为红,交换pParent和pBrother的颜色
 88                 SwapRBTreeNodeColor(pParent, pBrother);
 89                 return;
 90             }
 91         }
 92         if (pBrotherRight->isRed && !pBrotherLeft->isRed) {
 93             //情况5：兄弟节点的左子节点为红，右子节点为黑, 此时转化为情况4
 94             //将pBrother右旋转
 95             pBrother = RBTreeLeftRotate(pRoot, pBrother);
 96 
 97             pBrotherLeft = pBrother->pLeft;
 98 
 99             //交换颜色
100             SwapRBTreeNodeColor(pBrother, pBrotherLeft);
101         }
102         if (pBrotherLeft->isRed) {
103             //情况4：先左旋转pParent
104             RBTreeNode* pGrandParent = RBTreeRightRotate(pRoot, pParent);
105             pParent = pGrandParent->pRight;
106 
107             //交换颜色
108             SwapRBTreeNodeColor(pGrandParent, pParent);
109 
110             //将pBrotherRight标黑
111             pBrotherLeft->isRed = RBTreeNodeBlack;
112         }
113     }
114 }

红黑树（二）：删除

标签：不可 pre node 最大改变分享图片 pmi 导致平衡

原文地址：https://www.cnblogs.com/zengyg/p/9030053.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行