关于二叉查找树的一些事儿（bst详解）

标签：排序   详解   info   电脑   现在   期望   ati   lse   代码   

最近刚学了平衡树，然后突发奇想写几篇博客纪念一下，可能由于是刚学的缘故，还有点儿生疏，望大家海涵

说到平衡树，就不得不从基础说起，而基础，正是二叉查找树

什么是二叉查找树？？

大家观察一下下面的这棵二叉树

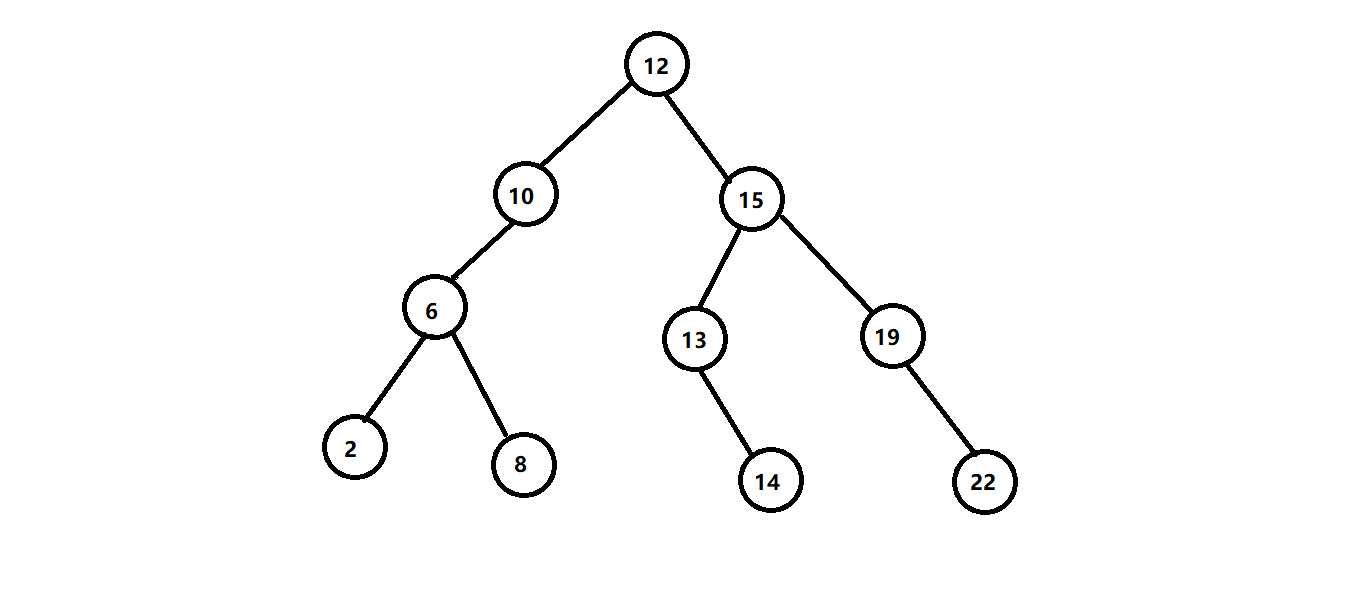
相信大家一眼就能发现，这棵树从左往右是递增的（也就是右儿子大于左儿子）

那么这样的一棵树有什么用呢？

就比如说图上的这个数列 12 10 15 6 13 19 2 8 14 22

如果你想找第n大的数，你明显需要冒泡或排序最坏O（n^2/2），O（nlogn）；

如果数列在更改一下，那你每次都要跑这么多，电脑累死了

但如果你用上图这棵树，根据他（右儿子>自己>左儿子）的特性，可以在期望复杂度O（logn）的时间内查出一个数据

同时修改也变得简单，O（logn）的时间查找位置，O（1）的时间连边

如下图解释

这次我要插入7，我们从根节点开始

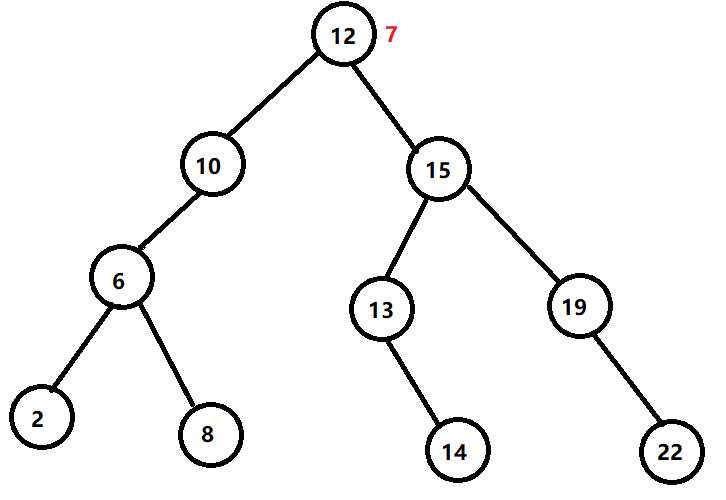
很明显，根节点大于7，那么我把7下放到左儿子

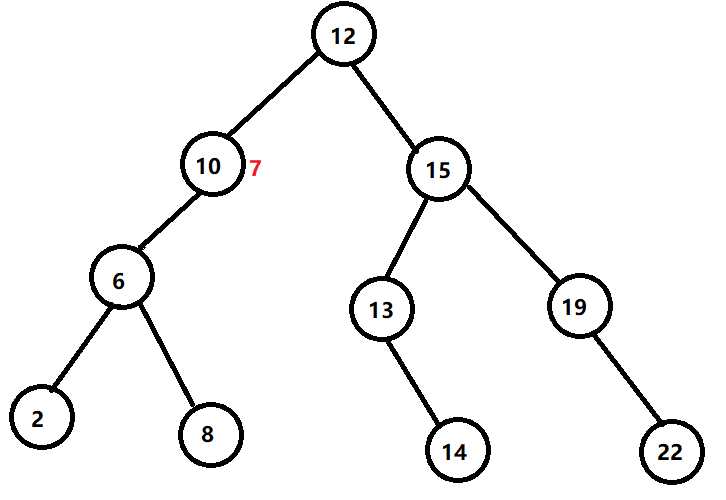
还是大，怎么办？继续下放到左儿子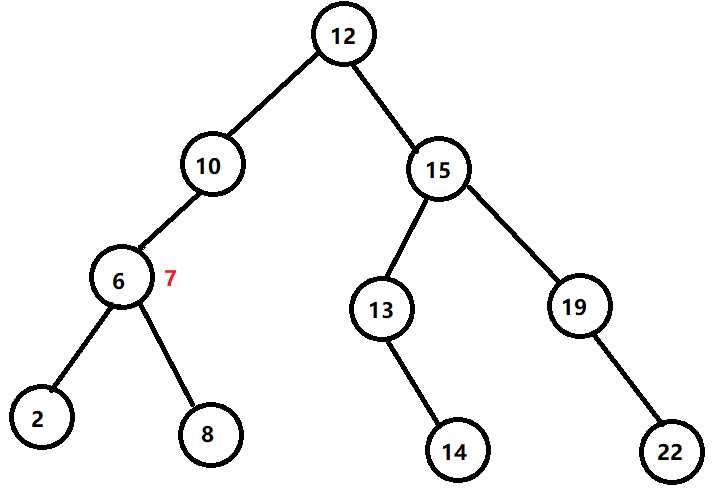

 这次是小了，放右儿子

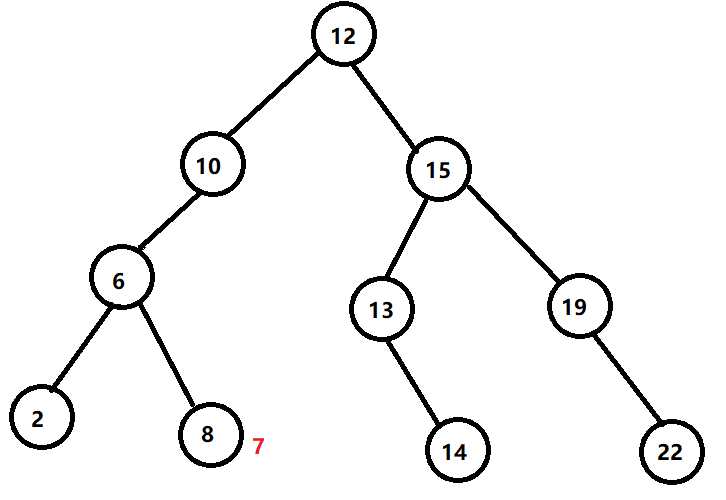
右儿子又大了，我们把他往左儿子上放

 但是，8这里没有左儿子

可以恭喜了，7终于找到了自己的位置，我们现在新建一个结点，连一条边，使他变为8的左儿子

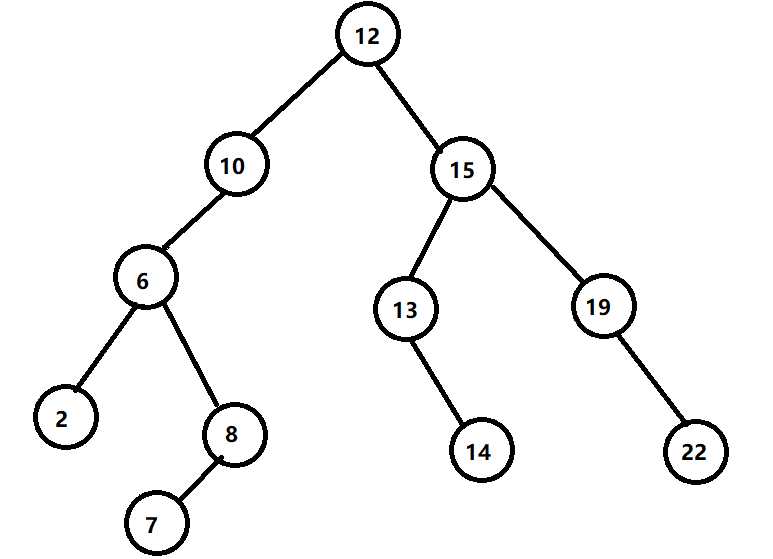
当然，有重复时也很好办，在该结点加一个数量标记，告诉他有几个即可

 插入的代码：

void add(int wz,int v)
{
	x[wz].size++;
	if(x[wz].val==v)
	{
		x[wz].cnt++;
		return;
	}
	if(x[wz].val>v)
	{
		if(x[wz].ls!=0)
		{
			add(x[wz].ls,v); 
		} 
		else
		{
			bnt++;
			x[bnt].val=v;
			x[bnt].size=1;
			x[bnt].cnt=1;
			x[wz].ls=bnt;
		}
	}
	else
	{
		if(x[wz].rs!=0)
		{
			add(x[wz].rs,v);
		}
		else
		{
			bnt++;
			x[bnt].val=v;
			x[bnt].size=1;
			x[bnt].cnt=1;
			x[wz].rs=bnt;
		}
	}
}

　　未完待续（其实是没来得及写完），如有问题欢迎指出

关于二叉查找树的一些事儿（bst详解）

标签：排序   详解   info   电脑   现在   期望   ati   lse   代码   

原文地址：https://www.cnblogs.com/ztz11/p/9030674.html