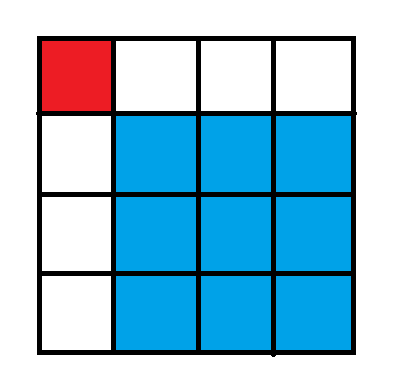
今天跳跳去公园游玩,第一个游戏就难倒了跳跳,游戏规则是跳跳站在一个面积无限大的矩形土地上,开始时跳跳在左上角(即第一行第一列),每一次跳跳都可以选择一个右下方格子,并瞬间跳过去(如从下图中的红色格子能直接跳到蓝色格子),求跳到第n行第m列的格子有多少种方案,答案对1000000007取模。
标签:bit == 多少 矩形 规律 解决 ++ 游戏 can
今天跳跳去公园游玩,第一个游戏就难倒了跳跳,游戏规则是跳跳站在一个面积无限大的矩形土地上,开始时跳跳在左上角(即第一行第一列),每一次跳跳都可以选择一个右下方格子,并瞬间跳过去(如从下图中的红色格子能直接跳到蓝色格子),求跳到第n行第m列的格子有多少种方案,答案对1000000007取模。

单组测试数据。
两个整数n,m(2<=n,m<=100000)
一个整数表示方案数。
4 5
10
组合数解决,可以发现规律当(2,2)是起点时,dp[x][y] = dp[x-1][y] + dp[x][y-1] ,跟51nod1118可以说是很像了
#include <bits/stdc++.h> using namespace std; typedef long long LL; LL mod = 1000000007; LL pow(LL a,LL b) { LL ans=1; while(b) { if(b&1) ans=(ans*a)%mod; a=(a*a)%mod; b>>=1; } return ans; } LL C(LL n,LL m) { LL i; if(m==0) return 1; if(m>n-m) m=n-m; LL up=1,down=1; for(i=1; i<=m; i++) { up=(up*(n-i+1))%mod; down=(down*i)%mod; } return up*pow(down,mod-2)%mod; } LL lucas(LL n, LL m) { if(m==0) return 1; return lucas(n/mod,m/mod)*C(n%mod,m%mod)%mod; } int main() { LL m, n, t; scanf("%lld%lld", &n, &m, &mod); n--, m--; printf("%lld\n", lucas(n+m-2, min(n-1, m-1))); return 0; }
标签:bit == 多少 矩形 规律 解决 ++ 游戏 can
原文地址:https://www.cnblogs.com/lesroad/p/9032925.html