标签:特性 查找 绝对值 现在 大于 import app letter ros
AVL是平衡二叉查找树,它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
若将二叉树结点上的平衡因子BF(Balance Factor)定义为该结点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有结点的平衡因子只能是-1,0,1。
平衡二叉查找树,在添加或者删除的结点的过程中,如果失去平衡,则需要进行平衡调整。调整的过程中,要保持根大于左,小于右的特性。
最早的平衡二叉树之一。应用相对其他数据结构比较少。windows对进程地址空间的管理用到了AVL树。
以后遇到再说。
B-树是一种平衡的多路查找树。B-树中所有结点孩子结点个数的最大值称为B-树的阶,通常用m表示,从查找效率考虑,要求m>=3。
一颗m阶的B-树,或者为空树,或为满足下面特性的m叉树:
(1)树中每个结点至多有m课子树。
(2)若根结点不是叶子结点,则至少有两颗子树。
(3)除根之外的所有非叶子结点至少有m/2(向上取整)颗子树。
(4)所有的非叶子结点内关键字互不相等,且从小到大排列。
(5)所有叶子结点都出现在同一层次上,并且不带信息(可以用空指针表示),可以看做查找失败到达的位置。
如图,m为3,3阶B-树
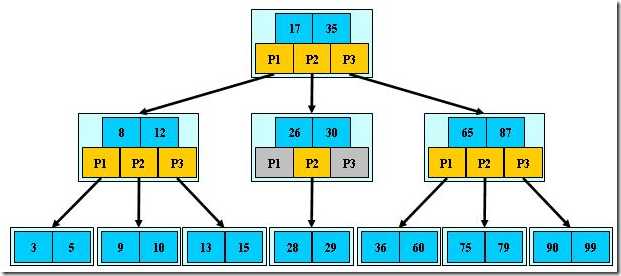
(1)B-树中,具有n个关键字的结点含有n+1个分支。
(2)m阶B-树中,每个结点(除根结点以外)中,关键字的个数是{m/2(向上取整)-1}<= n <= m-1。根结点的关键字个数是1<= n <=m-1。
(3)在B-树中,下层结点的关键字取值总是落在 由上层关键字所划分的区间内。
下图,如每个结点的结构,n为关键字的个数,P该节点的孩子结点,P1的取值范围 是小于K1,P2的取值范围 是大于K1 小于K2 依次类推
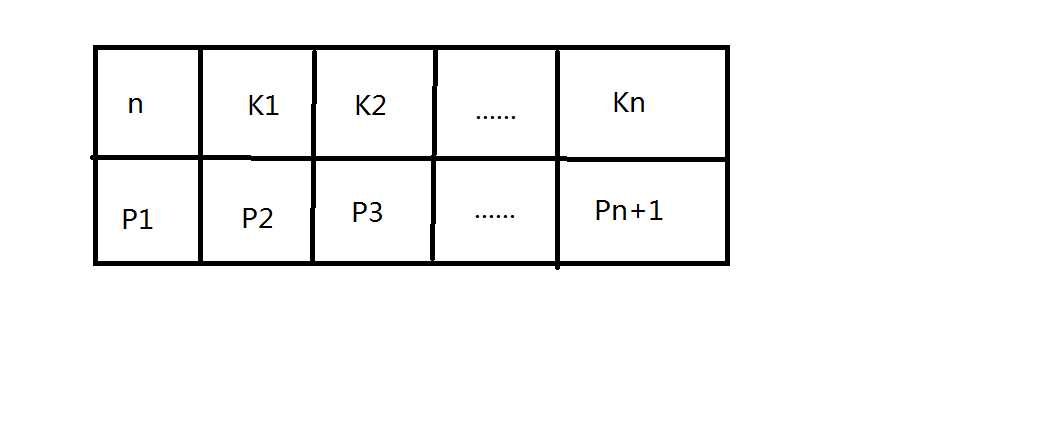
MongoDB为什么使用B-树,可以从它的设计角度来考虑,它并不是传统的关系性数据库,而是以Json格式作为存储的nosql,目的就是高性能,高可用,易扩展。它摆脱了关系模型,MongoDB 是聚合型数据库,而 B-树恰好 key 和 data 域聚合在一起。MongoDB使用B-树,所有节点都有Data域,只要找到指定索引就可以进行访问,无疑单次查询平均快于Mysql(但侧面来看Mysql至少平均查询耗时差不多)。
尽可能少的磁盘 IO 是提高性能的有效手段。
对于B-树的插入操作,B-的插入总是发生在叶子结点上,为了保持B-树的特性,有结点拆分(取中间关键字,独立成根结点或并入根结点)。
对于B-树的删除操作,为了保持B-树的特性和删除的操作应发生在最下层的叶子结点上,有与叶子结点交换关键字,有向兄弟结点借关键字,有结点合并的操作。
可以参考https://blog.csdn.net/qq_23217629/article/details/52510485
B-树和B+树最重要的一个区别就是B+树只有叶节点存放数据,其余节点用来索引,而B-树是每个索引节点都会有Data域。这就决定了B+树更适合用来存储外部数据,也就是所谓的磁盘数据。
标签:特性 查找 绝对值 现在 大于 import app letter ros
原文地址:https://www.cnblogs.com/weiziqiang/p/9038318.html