标签:page 相等 div 正整数 经纬 abstract 分数 分组 info
1.复合数据
2.数据抽象
3.抽象壁垒
复合数据:将多个数据绑定在一起,如日期、经纬度。
函数为数据的表示与操作构建抽象壁垒的方法论。
数据抽象允许我们将符合数据视作操作的基本单位。
数据抽象将数据的表示与操作分离开:
-单个数据如何表示为一个整体(as parts)
-作为一个整体的数据如何进行操作(as unit)
以程序来表示分数间的各种操作(假设分子和分母都为正整数)
首先,分数由两部分组成,numerator(分子)和denominator(分母),其为一对数值,即复合数据。写作:

要对两个分数进行运算,必须对其分子和分母进行相应操作。
那么如何表示作为整体(unit)的分数与部分的分子与分母?其实现暂且不论,就结果来看,要实现的是这样一种效果:
![]() rational函数返回一个分数
rational函数返回一个分数
 number和denom函数分别返回这个分数的分子与分母
number和denom函数分别返回这个分数的分子与分母
因为rational是构造分数的方法,因此称之为Constructor;
numer和denom是从数据对(分数)中选择特定部分的方法,因此称之为Selector。
仍旧不去管如何实现,只以此为基础完成基本操作。(这里只实现加、乘、比较相等与格式化打印的操作)
图示如下:
![]()
![]()
def mul_rational(x, y): return rational(numer(x) * numer(x), denom(x) * denom(x)) def add_rational(x, y): nx, ny = numer(x), numer(y) dx, dy = denom(x), denom(y) return rational(nx * dy + ny * dx, dx * dy) def equal_rationals(x, y): return numer(x) * denom(y) == denom(x) * numer(y) def print_rational(x): print(numer(x), ‘/‘, denom(x))
接下来我们再完成各个函数的实现
首先我们先以形如[n, d]的列表形式表示分数
from fractions import gcd # 以列表表示分数 # Constructor def rational(n, d): g = gcd(n, d) return [n//g, d//g] # 由分数求得分母 # Selector def numer(x): return x[0] # 由分数求得分子 # Selector def denom(x): return x[1]
如果换一种分数的表示方式呢?这次用函数来表示一个分数,以特定参数调用函数表示分母和分子。
即便改变如此之大,高一层的抽象,即分数间的操作是不用做任何改变的,要改变的只是分数及其部分的表示形式。
# 以函数表示分数 # Constructor def rational(n, d): def select(name): if name == ‘n‘: return n elif name == ‘d‘: return d return select # Selector def numer(x): return x(‘n‘) # Selector def denom(x): return x(‘d‘)
以上的代码中,用两种方式实现了分数及其部分的实现方法,但建诸其上的分数操作却完全不用改变。
这里就涉及到了抽象的层级。在当前问题的语境内可以分隔出以下的抽象层级:
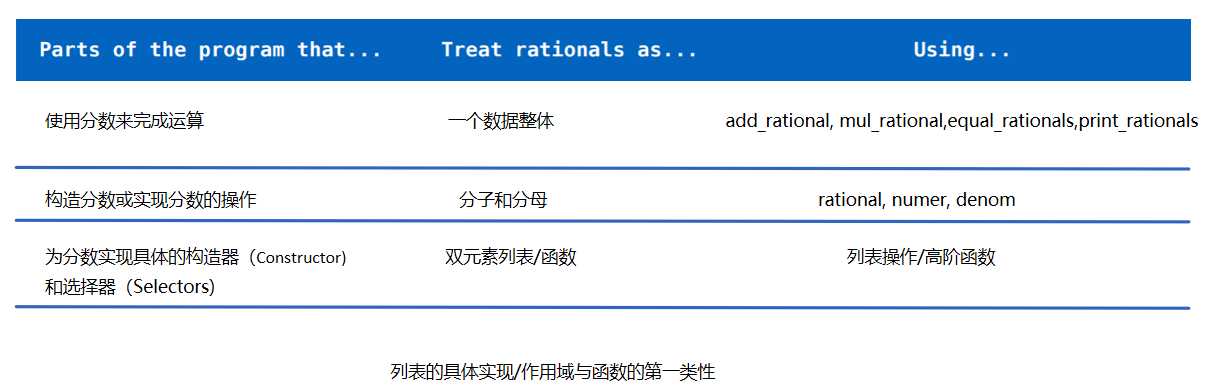
各抽象层级间的粗线表示抽象层级间的壁垒。在实现程序时,不要实现去做跨越层级的操作,如下图:

这样会使程序的抽象结构慌乱不堪,程序也因之变得脆弱。一旦要对某一部分进行修改,整个程序都会不再稳定。
https://cs61a.org/assets/slides/10-Data_Abstraction_1pp.pdf
http://composingprograms.com/pages/21-introduction.html
《改变:问题形成和解决的原则》中关于第二序改变的论述
标签:page 相等 div 正整数 经纬 abstract 分数 分组 info
原文地址:https://www.cnblogs.com/yifeixu/p/9038559.html