竞赛图的一些性质

标签：否则   参考   class   完全   sdn   lan   tail   bubuko   bin   

如果有错误请指出, 谢谢

定义

竞赛图 : \(\binom n 2\) 条边的有向图 (完全图)

定理 1

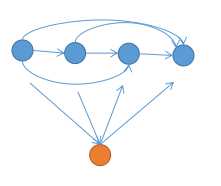
竞赛图强连通缩点后的DAG呈链状, 前面的所有点向后面的所有点连边

证明 : 考虑归纳, 逐连通块加入
目前有一条链, 插入一个新连通块x
如果x连向所有点, 放在链头
如果所有点连向x, 放在链尾
否则x的出边一定都在x的入边的后边 (否则成环)
找到分界点, 把x插在中间即可

定理 2

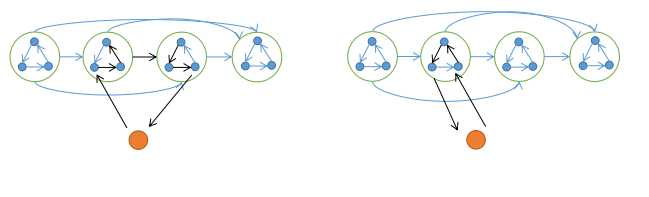
竞赛图的强连通块 存在一条哈密顿回路

证明 : 考虑归纳, 逐点加入
目前有一条链, 链上的每个强连通块都存在哈密顿回路
插入一个新点x, 只需证明新图中的强连通块都存在哈密顿回路即可
如果不产生新连通块, 就是定理 1 中讨论的情况, 否则一定存在一条x的出边在x入边左边, 随便找一对
如果是连到不同连通块, 见左图.
如果是同一连通块, 必定存在符合环的走向的相邻的一入一出, 见右图.

定理 3

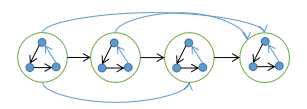
竞赛图存在一条 哈密顿路径

证明 : 如图示方法构造

引理

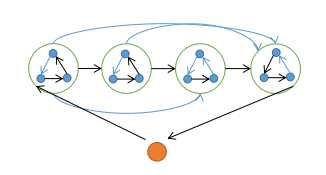
竞赛图里, 大小为 \(n>1\) 的强连通块中, 大小为 \([3, n]\) 的简单环均存在

证明 :
n=3成立, n$\ge$4时只需证明存在大小为 \(n-1\) 的就好了
考虑从原图中提出一个点, 剩下的图是一条链, 提出来的点有出边指向链头, 有来自链尾的入边.
如果剩下的图只有一个强连通块, 那么大小为 \(n-1\) 的环已经存在了.
只需考虑至少两个强连通块的情况, 如图示方法构造
(在定理3构造的哈密顿路径中, 是一段环边一条链边这样走的, 将一段环边的起点/终点删掉.)

定理4

竞赛图判定定理 Landau‘s Theorem:
未完待续

参考资料

[竞赛图判定定理]兰道定理(Landau‘s Theorem)介绍及其一种证明

竞赛图的一些性质

标签：否则   参考   class   完全   sdn   lan   tail   bubuko   bin   

原文地址：https://www.cnblogs.com/acha/p/9042984.html