标签:acm
这道题弄了很久,网上的很多都看不懂,所以想要写一个像我这种菜鸟都可以看得懂的解析。题意是将一个长度为n的序列,分成m段不相交叉的子段,使得他们的和最大。
于是可以用dp[i][j]来表示在前j个数中,以num[j]结尾并分为i段的最大和。此时我们可以得出一个式子,dp[i][j]=max(dp[i-1][k]+a[j],dp[i][j-1]+a[j]) (i-1< k< j-1)。分别表示num[j]单独成段和num[j]加入以num[j-1]结尾的一段。
现在举一个例子,序列为-1,4,-2,3,-2,3。
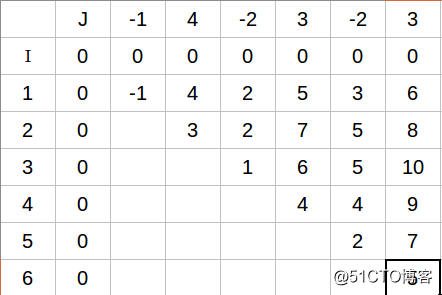
现在可以结合图标来理解式子的意思了,例如dp[2][4]=max(max(-1,4,2,) , 2)+num[4]=7
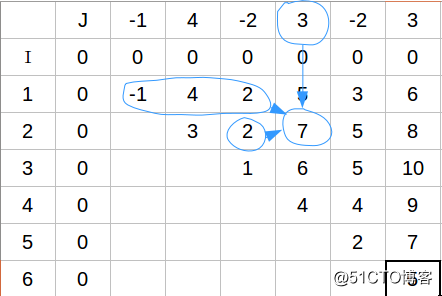
也就是说计算dp[i][j]只用到了2层的数据,上一层的数据我们只用到了其中的最大值,于是在求dp[j]时,我们可以用premax[]来记录i~j的最大值,在下一层时使用。
为什么i=n时,从第n位开始有值呢?因为这是每个数字自己单独成一段的情况,是满足分成n段的必要条件。
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn=1000000;
int num[maxn],premax[maxn],dp[maxn];
int main(){
int n,m,temp;
while(~scanf("%d %d",&m,&n)){
for(int i=1;i<=n;i++) scanf("%d",&num[i]);
memset(dp,0,sizeof(dp));
memset(premax,0,sizeof(premax));
for(int i=1;i<=m;i++){
temp=-1e9;
for(int j=i;j<=n;j++){
dp[j]=max(premax[j-1],dp[j-1])+num[j];
premax[j-1]=temp;//temp存放的是i~j-1中的最大值
temp=max(temp,dp[j]);
}
}
printf("%d\n",temp);
}
return 0;
}hdu 1024 Max Sum Plus Plus 小白都可以看得懂的解析
标签:acm
原文地址:http://blog.51cto.com/13688928/2117013