标签:五个 break desc names 要求 ima NPU AC turn
「BZOJ1485」[HNOI2009] 有趣的数列
Description
我们称一个长度为2n的数列是有趣的,当且仅当该数列满足以下三个条件:
(1)它是从1到2n共2n个整数的一个排列{ai};
(2)所有的奇数项满足a1<a3<…<a2n-1,所有的偶数项满足a2<a4<…<a2n;
(3)任意相邻的两项a2i-1与a2i(1≤i≤n)满足奇数项小于偶数项,即:a2i-1<a2i。
现在的任务是:对于给定的n,请求出有多少个不同的长度为2n的有趣的数列。因为最后的答案可能很大,所以只要求输出答案 mod P的值。
Input
输入文件只包含用空格隔开的两个整数n和P。输入数据保证,50%的数据满足n≤1000,100%的数据满足n≤1000000且P≤1000000000。
Output
仅含一个整数,表示不同的长度为2n的有趣的数列个数mod P的值。
Sample Input
3 10
Sample Output
5
对应的5个有趣的数列分别为(1,2,3,4,5,6),(1,2,3,5,4,6),(1,3,2,4,5,6),(1,3,2,5,4,6),(1,4,2,5,3,6)。
题解
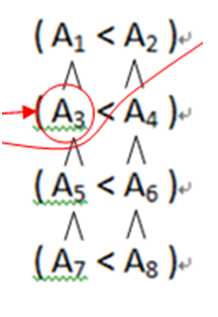
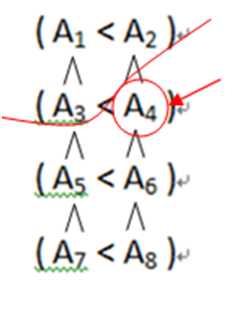
对于 A4 来说 它一定大于前三个
对于 A3 来说 它一定小于后五个
所以可以推断 AI <2*i
可以容易得到一个n^2的dp
f[i][j]表示前i位填到数字j的方案,即第i位用的是j
f[i][j]=f[i][j-1]+f[i-1][j-1] (j<=2*i-1)
f[i][j]=f[i][j-1] (j>2*i-1)
输出前几项,发现是个卡特兰数列 F(n)=C(2*n,n)/(n+1)
分解质因数求即可
至于为什么是卡特兰数列?其实就是从左往右扫每个数,把放在奇数项看作入栈,偶数看作出栈
50 分 dp
#include<bits/stdc++.h> using namespace std; int n,mod; int f[1005][2005]; int main(){ scanf("%d%d",&n,&mod); for(int i=0;i<=2*n;i++) f[0][i]=1; for(int i=1;i<=n;i++) for(int j=1;j<=2*n;j++) if (j<=2*i-1) f[i][j]=(f[i][j-1]+f[i-1][j-1])%mod; else f[i][j]=f[i][j-1]%mod; printf("%d\n",f[n][2*n]); return 0; }
100 分 卡特兰
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int MAXN=1e6+5; ll pri[MAXN],mn[MAXN*2],num[MAXN*2],ans=1; int n,mod,cnt; bool use[MAXN*2]; void getpri(){ for (int i=2;i<=2*n;i++){ if (!use[i]) pri[++cnt]=i,mn[i]=cnt; for (int j=1;pri[j]*i<=2*n&&j<=cnt;j++){ use[pri[j]*i]=1,mn[pri[j]*i]=j; if (i%pri[j]==0) break; } } } void add(int x,int f){ while (x!=1){ num[mn[x]]+=f; x/=pri[mn[x]]; } } int main(){ scanf("%d%d",&n,&mod); getpri(); for (int i=2*n;i>n;i--) add(i,1); for (int i=1;i<=n;i++) add(i,-1); add(n+1,-1); for (int i=1;i<=cnt;i++) while (num[i]--) ans=(ans*pri[i])%mod; printf("%lld\n",ans); return 0; }
「BZOJ1485」[HNOI2009] 有趣的数列 卡特兰数列
标签:五个 break desc names 要求 ima NPU AC turn
原文地址:https://www.cnblogs.com/shjrd-dlb/p/9048894.html