We have a large square grid with H rows and W columns. Iroha is now standing in the top-left cell. She will repeat going right or down to the adjacent cell, until she reaches the bottom-right cell.
However, she cannot enter the cells in the intersection of the bottom A rows and the leftmost B columns. (That is, there are A×B forbidden cells.) There is no restriction on entering the other cells.
Find the number of ways she can travel to the bottom-right cell.
Since this number can be extremely large, print the number modulo 109+7.
Constraints
1≤H,W≤100,000
1≤A<H
1≤B<W
We have a 2×3 grid, but entering the bottom-left cell is forbidden. The number of ways to travel is two: "Right, Right, Down" and "Right, Down, Right".
思路:总的走法减去错误走法;总的走法数为f((1,1)—>(h,w))(记f((a,b)—>(c,d))为从(a,b)走到(c,d)的走法数),错误的走法数为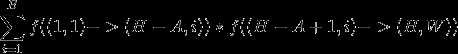 (公式含义易看出)
(公式含义易看出)
AC代码:
#include <iostream>
#include<cstdio>
#include<algorithm>
const long long mod=1e9+7;
typedef long long ll;
using namespace std;
ll f[1000010],revf[1000010];//数组大小至少要为1e5*2
ll qpow(ll a,ll b){
ll ret=1;
while(b){
if(b&1) ret=(ret*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ret;
}
void init(){
f[0]=1; revf[0]=qpow(f[0],mod-2);
for(ll i=1;i<1000010;i++){
f[i]=i*f[i-1]%mod;
revf[i]=qpow(f[i],mod-2);
}
}
ll C(ll n,ll m){
return (f[n]*revf[m])%mod*revf[n-m]%mod;
}
ll count_ways(ll a,ll b,ll c,ll d){
ll tot=(c-a)+(d-b);
ll down=(c-a);
ll ret=C(tot,down);
return ret;
}
int main()
{
init();
ll h,w,a,b;
cin>>h>>w>>a>>b;
ll tot=count_ways(1,1,h,w);
for(ll i=1;i<=b;i++){
ll tmp=count_ways(1,1,h-a,i)*count_ways(h-a+1,i,h,w)%mod;
while(tot<tmp) tot+=mod;//防止出现负数
tot=(tot-tmp)%mod;
}
cout<<tot<<endl;
return 0;
}

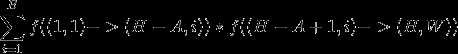 (公式含义易看出)
(公式含义易看出)