标签:cto code ORC codeforce max name img fine 现在
题意略。
思路:构造题。
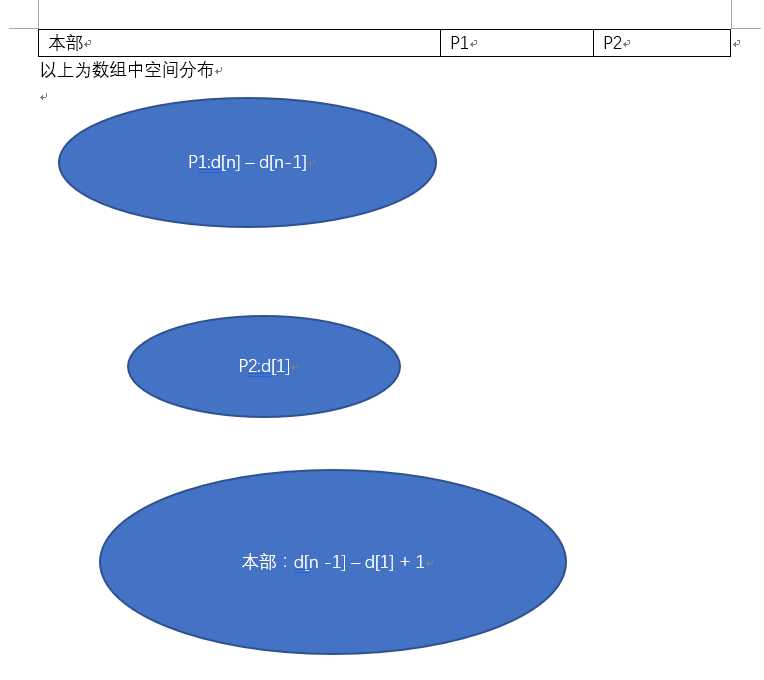
我们把全部的d[n]+1个点分作3部分来构造。
首先我们把原问题归约成构造d1、dn、和{d2 - d1,d3 - d1,.....,d[n-1] - d1}这样的问题,其中第三部分的构造相当于是原问题的子问题。
1.由本部向P2中每一个点都连接一条边,这样可以补上第三部分中每个元素都缺少的d1,现在相当于构造出了{d2,d3,....,d[n - 1]},还差d1和dn没构造出来。
2.用剩下的dn - d[n-1]来凑d1,P1向P2中每个点都连一条边,可以凑出d1。
3.现在P2内的点的度为dn - d[n-1] + d[n-1] - d1 + 1 = dn - (d1 - 1)。如果将P2内的点连成一个完全图,可以补上(d1 - 1),从而得到dn的值。
递归时的边界条件为l > r,或l == r。
1.l > r时,rst = 1,什么都不做就行。
2.l == r时,rst = d[l] + 1,将它连成一个完全图即符合题意。
rst表示当前问题的本部部分有多少个点,从而确定P1和P2在数组中的下标起始。
详见代码:
#include<bits/stdc++.h> #define maxn 350 #define maxn1 1050 using namespace std; int di[maxn],rst,n,cnt; vector<int> graph[maxn1]; void dfs(int l,int r){ if(l > r){ rst = 1; return; } if(l == r){ for(int i = 1;i <= di[l] + 1;++i){ for(int j = i + 1;j <= di[l] + 1;++j){ graph[i].push_back(j); ++cnt; } } rst = di[l] + 1; return; } int p1 = di[r] - di[r - 1],p2 = di[l]; for(int i = l + 1;i <= r - 1;++i) di[i] -= di[l]; dfs(l + 1,r - 1); for(int i = 1;i <= rst;++i){ for(int j = rst + p1 + 1;j <= rst + p1 + p2;++j){ graph[i].push_back(j); ++cnt; } } for(int i = rst + 1;i <= rst + p1;++i){ for(int j = rst + p1 + 1;j <= rst + p1 + p2;++j){ graph[i].push_back(j); ++cnt; } } for(int i = rst + p1 + 1;i <= rst + p1 + p2;++i){ for(int j = i + 1;j <= rst + p1 + p2;++j){ graph[i].push_back(j); ++cnt; } } rst += (p1 + p2); for(int i = l + 1;i <= r - 1;++i) di[i] += di[l]; return; } int main(){ scanf("%d",&n); for(int i = 1;i <= n;++i){ scanf("%d",&di[i]); } dfs(1,n); printf("%d\n",cnt); for(int i = 1;i <= di[n];++i){ for(int j = 0;j < graph[i].size();++j){ printf("%d %d\n",i,graph[i][j]); } } return 0; }
标签:cto code ORC codeforce max name img fine 现在
原文地址:https://www.cnblogs.com/tiberius/p/9055535.html