毕业设计总结（2）-拟合曲线模拟障碍物

标签：style   blog   http   color   io   使用   ar   strong   for   

　　 1. 简要介绍

　　首先贴出前面的文章地址：【毕业设计总结（1）】

　　我们再复习一下题目的要求：在一个布满障碍物的地图上，过凸极值点划分区域；在相应的区域中抽象出一个点来对应各区域，画出连通无向图；根据对应的权值找出最优路径；写出相应的算法。

　　障碍物是我们使用算法拟合出来的，而不是在canvas上默认已经有了障碍物。基本的步骤就是根据canvas上一些散列的点，拟合出一条平滑的、封闭的曲线，这就是传说中的【曲线拟合】，曲线拟合最常用的就是贝赛尔曲线和最小二乘法了。这里我使用的就是贝赛尔曲线进行拟合。

　　第二节的内容相信大家应该都看到过！就当复习一遍的啦！

　　 2. 贝塞尔曲线

　　 2.1 定义

　　在数学的数值分析领域中，贝塞尔曲线（英语：Bézier curve）是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面，其中贝塞尔三角是一种特殊的实例。

　　贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发，以稳定数值的方法求出贝塞尔曲线。

　　 2.2 公式

　　线性贝塞尔曲线：

　　给定点P₀、P₁，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出：

 　　我们可以通俗点理解：平面中有两个点P0(x0, y0), P1(x1, y1)，那么线性的贝赛尔曲线就是

　　B(x) = x₀ + (x₁-x₀)t = (1-t)x₀ + tx₁;

　　B(y) = y₀ + (y₁-y₀)t = (1-t)y₀ + ty₁;

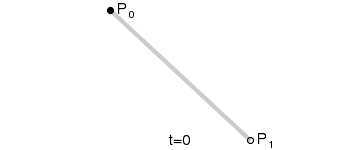
　　二次贝赛尔曲线：

　　二次方贝塞尔曲线的路径由给定点P₀、P₁、P₂的函数B（t）追踪：

　　。

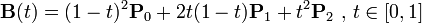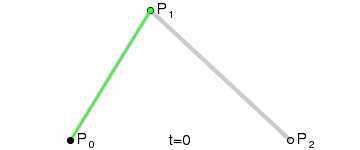
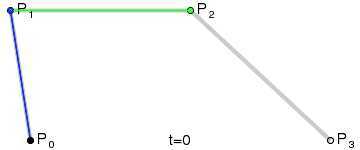
 　　三次方贝塞尔曲线

　　P₀、P₁、P₂、P₃四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P₀走向P₁，并从P₂的方向来到P₃。一般不会经过P₁或P₂；这两个点只是在那里提供方向资讯。P₀和P₁之间的间距，决定了曲线在转而趋进P₃之前，走向P₂方向的“长度有多长”。

　　曲线的参数形式为：

　　。

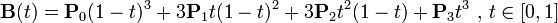　　三次贝塞尔曲线需要四个控制点才能画出来。用x,y 表示更容易我们的理解：

　　B(x) = x₀(1-t)³ + 3x₁t(1-t)² + 3x₂t²(1-t) + x₃t³;

　　B(y) = y₀(1-t)³ + 3y₁t(1-t)² + 3y₂t²(1-t) + y₃t³;

　　根据t的变化，我们能够求出贝赛尔曲线上的各个不连续的点。

　　 2.3 特性

• 开始于P₀并结丛于P_n的曲线，即所谓的端点插值法属性。
• 曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的，贝塞尔曲线是直线的充分必要条件是控制点共线。
• 曲线的起始点（结丛点）相切于贝塞尔多边形的第一节（最后一节）。
• 一条曲线可在任意点切割成两条或任意多条子曲线，每一条子曲线仍是贝塞尔曲线。
• 一些看似简单的曲线（如圆）无法以贝塞尔曲线精确的描述，或分段成贝塞尔曲线（虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时，分成四段的贝塞尔曲线，可以小于千分之一的最大半径误差近似于圆）。
• 位于固定偏移量的曲线（来自给定的贝塞尔曲线），又称作偏移曲线（假平行于原来的曲线，如两条铁轨之间的偏移）无法以贝塞尔曲线精确的形成（某些平凡实例除外）。无论如何，现存的启发法通常可为实际用途中给出近似值。
• 贝塞尔曲线在端点的切线，是平行于过端点和相邻控制点的连线。

　　好了，前面的都是知识储备，现在开始程序上的构造了。

　　 3. 拟合障碍物

　　我们需要的是边界平滑的障碍物，可是如果用特别高阶的贝塞尔曲线，又为后面的计算增加了很多的麻烦，于是我们的考虑是，用三次贝塞尔曲线平滑的连接，封闭成一个障碍物。

　　 在2.3特性中，有着特别重要的一条属性：“贝塞尔曲线在端点的切线，是平行于过端点和相邻控制点的连线”，利用这条特性，我们可以把两条相邻的三次贝赛尔曲线平滑的衔接在一起。

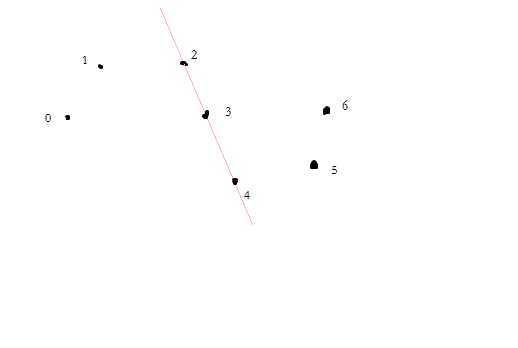
　　如下图（草图，将就着看看^_^）：0, 1, 2, 3组成三次贝赛尔曲线A，3, 4, 5, 6组成三次贝塞尔曲线B，而2, 3, 4在同一条直线上。根据刚才的特性我们就能知道曲线A和曲线B在点3处的切线肯定是同一条（点2, 3, 4），这样曲线A和曲线B在点3出就能平滑的过渡，同理更多的三次贝赛尔曲线。

　　这时，可能就要有人问了，我在画板上点点的时候，难道还要特别精准的把三个点 点到一条直线上么，好难哦！现在我们就来解决这个问题

　　 3.1 曲线连接

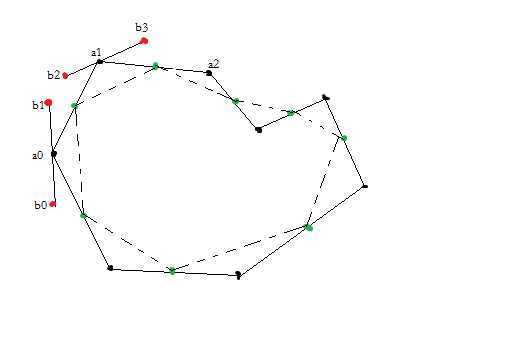
　　思路是：把所有相邻的点连接起来，然后取连线的中点，再连接起来，将中点连接起来的线段平移到之前的控制点上，以原始的相邻点为起点和终点，平移后的中点为控制点画贝赛尔曲线，就能保证相邻的贝赛尔曲线在衔接处是平滑的，同时贝塞尔曲线本身也是平滑，这样就能保证整条曲线都是平滑的了。

　　如下图，虚线是中点的连线，a0, a1是原始的点，b0, b1, b2, b3是中点，(a0, b1, b2, a1)就能一条三次贝塞尔曲线A的四个控制点，同理(a1, b3, b4, a2)也能画出一条贝塞尔曲线B。而b2,a1, b3又在同一直线上，那么曲线A和曲线B的交界必然是平滑相接的。

　　首先要做的就是获取所有的额外点（即上面所说的中点）

/*
 * 计算额外点的坐标
 * @param	points		[]		用户点击的点的坐标
 * @return	extrapoints	[]		额外点的坐标
 */
getExtra:function(points){
	var scale = 0.6;
	var t   = points.length;
	var mid = [];
	var m   = [];
	var extrapoints = [];
	//中间点
	for(var i=0; i<t; i++){
		var nexti = (i+t-1)%t;
		var x     = (points[i].x+points[nexti].x)/2.0;
		var y     = (points[i].y+points[nexti].y)/2.0;
		mid[i] = {'x':x, 'y':y};
	}
	for(var i=0; i<t; i++){
		var nexti = (i+1)%t;
		var x     = (mid[i].x+mid[nexti].x)/2.0;
		var y     = (mid[i].y+mid[nexti].y)/2.0;
		m[i] = {'x':x, 'y':y};
		
		var offsetx = points[i].x - m[i].x;
		var offsety = points[i].y - m[i].y;
		
		var j = i * 2;
		extrapoints[j] = {'x':mid[i].x + offsetx, 'y':mid[i].y + offsety};
		
		var ofx = (points[i].x - extrapoints[j].x)*scale;
		var ofy = (points[i].y - extrapoints[j].y)*scale;
		extrapoints[j].x = points[i].x - ofx;
		extrapoints[j].y = points[i].y - ofy;
		extrapoints[(j+1)%(2*t)] = {'x':points[i].x + ofx, 'y':points[i].y + ofy};
	}
	return extrapoints;
},

　　获取到额外点之后，我们就可以用原始点和额外点在构造曲线（障碍物）了，代码中有一个方法bezierkey.passPoints()这是要获取贝赛尔曲线上的点的坐标的，我们在3.2节中会讲到。

//points [[x0, y0, x1, y1, x2, y2, x3, y3], [x4, y4, x5, y5, x6, y6, x7, y7], ...]
drawBezier : function(points, extrapoints, color, lineWidth, fill){
	var t = points.length;
	var pp = [];
	
	var arr = [];
	for(var i=0; i<t; i++){
		var nexti = (i+1)%t;
		arr.push([points[i].x, points[i].y, extrapoints[i*2+1].x, extrapoints[i*2+1].y, extrapoints[nexti*2].x, extrapoints[nexti*2].y, points[nexti].x, points[nexti].y]);
		var p = bezierkey.passPoints(points[i], extrapoints[i*2+1], extrapoints[nexti*2], points[nexti]);
		pp = pp.concat(p);
	}
	jc.start('screen', true);
	jc('#srceen').lineStyle(lineWidth);
	jc.b3Curve(arr,color, fill);
	//jc.b3Curve([[points[i].x, points[i].y, extrapoints[i*2+1].x, extrapoints[i*2+1].y, extrapoints[nexti*2].x, extrapoints[nexti*2].y, points[nexti].x, points[nexti].y]], '#00ffbb');
	jc.start('screen', true);

	return pp;
},

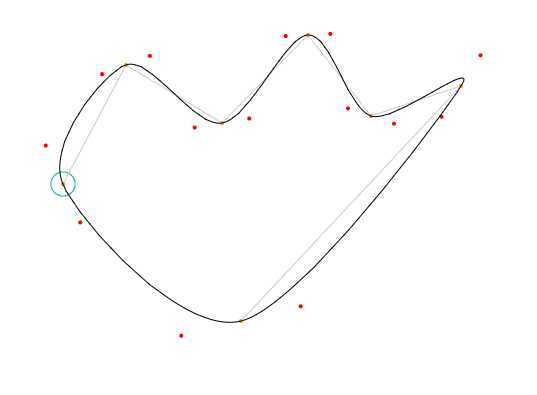
　　arr数组中的每个元素都是贝塞尔曲线的4个控制点，包括起始原点，额外点1，额外点2，终止原点。

　　画出的就是这个样子：橘色的小圆点是原始点，红色的小圆点是计算出的额外点，黑色的线就是贝塞尔曲线拼接出来的曲线

　　 3.2 获取曲线上的点的坐标

　　构造完成障碍物仅仅是视觉上完成了效果，可是在数学上，我们还不能进行计算呢，我们需要获取曲线上的点的坐标来为我们接下来的计算（计算凸极值点，过凸极值点做水平切线等）做准备。这时，我们上面的表达式就用到了：

　　B(x) = x₀(1-t)³ + 3x₁t(1-t)² + 3x₂t²(1-t) + x₃t³;

　　B(y) = y₀(1-t)³ + 3y₁t(1-t)² + 3y₂t²(1-t) + y₃t³;　　t[0, 1]

　　变换t的值，我们能够得到一系列的点，我设定的幅度是 t+= 0.01，即每条贝塞尔曲线上都取100个点的坐标，当然，这样设定的一个好处就是方便，不用根据每条曲线来设置相应的幅度；而缺点呢就是曲线长的点之间的距离就比较大，曲线短的点之间的距离就比较小。

/*
 * 计算由4个点确定的贝塞尔曲线都经过哪些点
 */
passPoints : function(point0, point1, point2, point3){
	var pp = [];
	
	for(var t=0.0; t<=1; t+=0.01){
		var x = Math.pow(1-t, 3)*point0.x + 3*Math.pow(1-t, 2)*t*point1.x + 3*Math.pow(t, 2)*(1-t)*point2.x + Math.pow(t, 3)*point3.x;
		var y = Math.pow(1-t, 3)*point0.y + 3*Math.pow(1-t, 2)*t*point1.y + 3*Math.pow(t, 2)*(1-t)*point2.y + Math.pow(t, 3)*point3.y;
		
		x = x.toFixed(4);	// 取小数点后4位
		y = y.toFixed(4);
		
		pp.push({'x':x, 'y':y, 'type':3});
	}
	return pp;
},

　　好了，目前我们已经构造出障碍物了，而且也能获取到障碍物上的点了，下一章开始讲解【曲线在y轴上的凸极值点和过凸极值点做水平切线】

　　 4 总结

　　前面的内容偏向理论，后面的内容偏向程序。当然，所有的理论都是为了能在实际中应用到。

　　如果哪里有不准确的地方，欢迎批评指正。

　　参考：

　　http://zh.wikipedia.org/wiki/%E8%B2%9D%E8%8C%B2%E6%9B%B2%E7%B7%9A

　　http://blog.csdn.net/microchenhong/article/details/6316332

毕业设计总结（2）-拟合曲线模拟障碍物

标签：style   blog   http   color   io   使用   ar   strong   for   

原文地址：http://www.cnblogs.com/xumengxuan/p/3993151.html