标签:题解 int 为什么 nbsp 不用 文本框 决定 时间复杂度 单位
题目描述如下:
经过几个月辛勤的工作,FJ 决定让奶牛放假。假期可以在 1…N 天内任意选择一段(需要连 续),每一天都有一个享受指数 W。但是奶牛的要求非常苛刻,假期不能短于 P 天,否则奶 牛不能得到足够的休息;假期也不能超过 Q 天,否则奶牛会玩的腻烦。FJ 想知道奶牛们能 获得的最大享受指数。 Input(holiday.in) 第一行:N,P,Q. 第二行:N 个数字,中间用一个空格隔开。 Output(holiday.out) 一个整数,奶牛们能获得的最大享受指数。
Sample Input 5 2 4 -9 -4 -3 8 -6
Sample Output 5
Limitation time:1s
memory:65536kb 50%
1≤N≤10000 100%
1≤N≤100000
1<=p<=q<=n Hint
选择第 3-4 天,享受指数为-3+8=5。
题解
这道题用到前缀和和RMQ,先来啰嗦一下RMQ
看了RMQ的PPT,我好像恍然大悟,弄懂了以前没有弄懂的式子。。
趁热来为自己写一下吧,免得明天就忘光了。
首先f[i][j]这个东西的含义和平常不同,它表示的是a[i]到a[i+2^j-1](咳咳注意这里的是2^j-1而不是2^(j-1)),之所以-1,当然是算上i啦,所以f[i][j]一共包含了2^j个数。然后通过代数,会发现2^j的一半是2^(j-1),这样,把一条含2^j个元素的线段拆成两半,每半含有的元素个数是2^(j-1)个。
现在看状态转移方程,就是让我懵了好久的方程,还好我自己反应过来了。
f[i][j]=max(f[i][j-1],f[i+2^(j-1)][j-1])
边界条件为f[i][0]=A[i]
起初菜菜的我不明白为什么两边都是j-1,现在我知道了,因为是2^(j-1)嘛!从i到i+2^(j-1)-1,元素个数为2^(j-1),这就和上述的解释对应上了,此时是求前半段的最大值;而后面的j-1,是在i+2^(j-1)这个数的基础上加的,也就是从i+2^(j-1)到i+2^(j-1)+2^(j-1)-1,嗯。。。不高深,只是我太菜。
至于边界条件,从a[i]到a[i+2^0-1]就是a[i],存的是a[i]的本身。
预处理f数组的时间复杂度就是O(NlgN)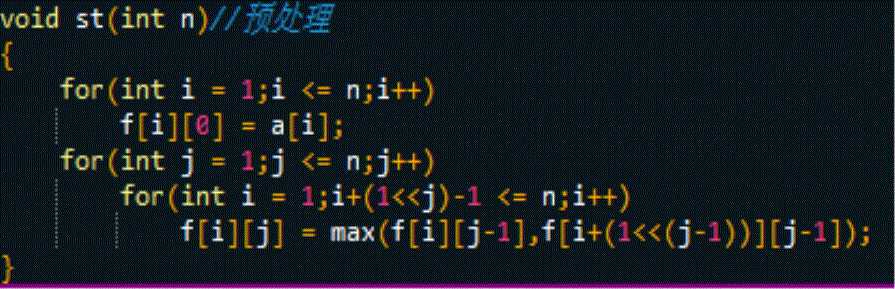
现在我要为这一页PPT写一页解析。
首先是第一行的2^x<=R-L+1。它只是题目中的一个条件,2^x是一个元素的个数(一个元素占一个单位那么它也就相当于长度了),小于区间的长度(R-L+1是区间的长度)。
如图所示,这里虽然把区间[L,R]分成了两部分,但并不是平分的,而是有一部分重叠的(但是两区间的长度还是一样的),所以上面文本框中的“2^j的一半是2^(j-1)”就用不到了,取而代之的,是[L,L+2^x-1](这个都懂,不用解释)。然后又让我发蒙的是下面的[R+1-2^x,R],别皱眉啊,这不就是把[R,R+2^x-1]中的2^x-1从右边挪到左边了吗?!,减过去就完事了。
最下面的式子也一样,x代表的是左边数的加上2^x-1这么多的数,并不是到x这个位置也不是这个数。吼吼吼,这个弄懂了,现在还剩的问题就是这个东西和
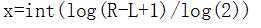 东西在int上的区别。。。根据张雪大佬
东西在int上的区别。。。根据张雪大佬
说,它是一个整数一个不一定是整数,但是如果一开始设x为整数的话这就没什么区别了。。。

好了啰嗦完毕,已经清楚的知道了RMQ。那么这道题的思路就是,先预处理出前缀和,然后在用RMQ求出前缀和i+p到i+q中的最大值(别忘了前缀和是从1到第i+p或第i+q天)(至于i枚举即可。,于是,求出这个最大值后,还要减去i的前缀和,就得到从i天开始休息的最大享受值。
end;
标签:题解 int 为什么 nbsp 不用 文本框 决定 时间复杂度 单位
原文地址:https://www.cnblogs.com/peppa/p/9059644.html