标签:soft color tair 楼梯 有关 加法 path rest family

费波那契数列由0和1开始,之后的费波那契系数就是由之前的两数相加而得出。
与斐波那契数列有关的问题,都符合这样的描述:
当前状态的得出是依赖于前两项的状态,给出初始状态F(0),F(1),之后的每一项都满足共同的特点,即为前两项状态相加。
前两项的状态,分别为当前状态的两种解法,适用加法原理。
下面给出几个例题:
1、Climbing Stairs 爬楼梯问题
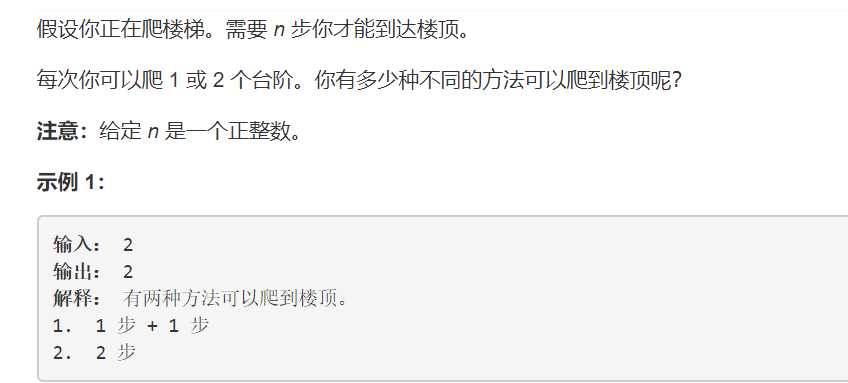
每次只能爬1或2步,那么爬到第n层的方法要么是从第n-1层一步上来的,要不就是从n-2层2步上来的,所以递推公式非常容易的就得出了:dp[n] = dp[n-1] + dp[n-2]

2、Unique Paths 不同路径问题

每次可以向下走或者向右走,求到达最右下角的所有不同走法的个数。需要用动态规划Dynamic Programming来解,我们可以维护一个二维数组dp,其中dp[i][j]表示到当前位置不同的走法的个数,然后可以得到递推式为: dp[i][j] = dp[i - 1][j] + dp[i][j - 1]

标签:soft color tair 楼梯 有关 加法 path rest family
原文地址:https://www.cnblogs.com/lidan-prime/p/9059715.html