Sparse Representation

标签：from   linear   its   orm   over   rom   wan   -o   HERE   

Given any signal \(x\in R^n\), we can obtain sparse representation \(\theta\in R^n\) of \(x\) in two ways:

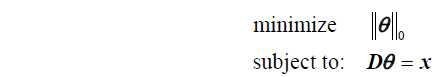1. Basis expansion: given sparse-inducing othonormal basis matrix \(B\in R^{n\times n}\), e.g., discrete cosine transform (DCT) matrix, iscrete wavelet transform (DWT) matrix, free-types filter banks of DWT etc. Precisely, we are finding sparse solution that satisfy:
   \[y=B\theta.\]
   2.Dictionary expansion: Given over complete dictionary \(D\in R^{n\times l}\) with \(l>n\), we want to a solution of
   \[D\theta=x\]
   Under the assumption of \(rank(D)=n\), we know there are infinite solutions. Among these representations of \(x\), we are particularly interested in finding the most economical one, \(\theta^*\) , that is the sparsest. Precisely, we need to solve:

(1)

It turns out that (1) is a problem of combinatorial complexity: finding solution of (1) requires
enumerating subsets of the dictionary to identify the smallest subset that can represent signal \(x\), the
complexity of such a subset search grows exponentially with \(l\). An important result concerning sparse
signals and compressed sensing is that under certain conditions the sparsest solution of $D\theta = x4 can be
obtained by solving the convex problem

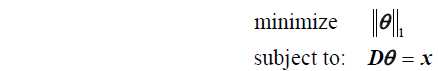（2）

If the data involved are all real-valued, (2) is equivalent to a linear program (LP), if the data are
complex-valued, then (1.15) is essentially a second-order cone program (SOCP). Hence (2) can be
solved effectively using any good convex program solvers like SeDuMi.

Examples of Dictionaries:

1. \(D=[I_n\; C_n^T]\), where \(I_n\) is the identity matrix of size \(n\times n\), \(C_n\) is the 1-D DCT matrix of size \(n\times n\).

2. \(D=[I_n\; W_n^T]\), where \(W_n\) is a 1-D DWT matrix.

[Remark]Compared to traditional basis expansion, dictionary based sparse model is more sparse. Secondly, it should be noticed that proper choice of dictionary is important, e.g, \(D=[I_n\; C_n^T]\) and \(D=[I_n\; W_n^T]\) are very representive.
That is to say, the dictionary is always composed of traditional orthonormal matrix.

Some terminology：
1.Dictionary: matrix \(D\)
2.Atom： columns of \(D\).
3.Overcomplete: \(n<l\)

1. A signal is said to be approximately sparse if it differs from a “nearby” sparse signal by a small amount in magnitude.
2. A signal is said to be compressible, if there exists a basis in which the signal admits approximately sparse representation.

Sparse Representation

标签：from   linear   its   orm   over   rom   wan   -o   HERE   

原文地址：https://www.cnblogs.com/mathlife/p/9060255.html