标签:box only classic lag AMM not which and src
Classic form of nonlinear programming
F1: \(f,h,g\) are arbitrary (not necessarily diferentiable or continuous) functions.

F2:
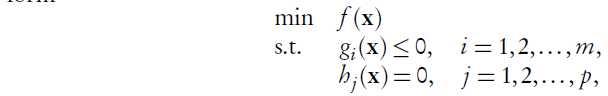
F3:
\[\begin{align*}
\min \; & f(x)\ \textrm{s.t.} \; & g(x)\leq 0\ & h(x)=0 \ & x\in X;
\end{align*}\]
As \(h(x)=0\) can be equivalently written as two inequality constraints \(h(x)\leq 0\) and \(-h(x)\leq 0\), we only consider
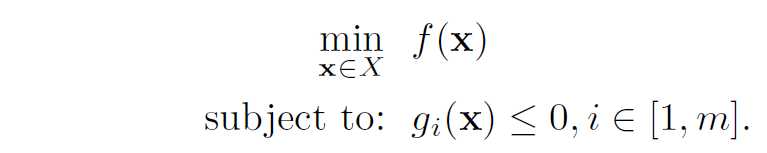
\(\color{red}{\mbox{Denote the primal domain by}}\) \(D=X\cap \{x|g(x)\leq 0, h(x)=0\}\).}
Lagrange function and its dual
1) Lagrange function:\(\mu \geq 0\) is called the Lagrange multiplier.
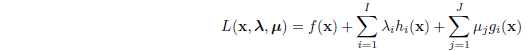
2)Lagrange dual function
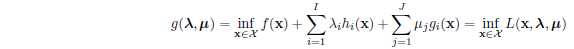
[Remark]Observe that the minimization to calculate the
dual is carried out over all \(x \in X\), rather than just those within the constraint set. For this reason, we can prove that for primal feasilbe \(x\in D\) and dual feasible \((\lambda, \mu \geq 0)\) , we have
\[g(\bar{\lambda},\bar{\mu})\leq f(\bar{x})\]
So we have for \(\mu \geq 0\) and \(x\in D\),
\[d^*=\sup g(\lambda,\mu)\leq \inf f(x)=f^*\],
which is called weak dual theorem.
Weak duallity
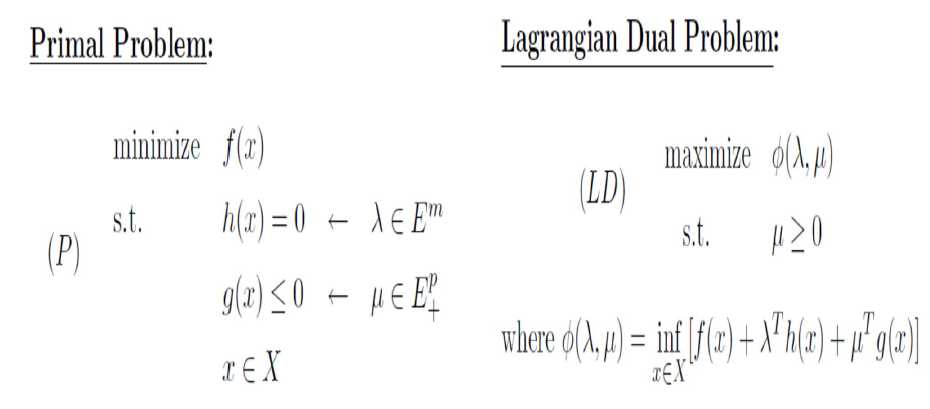


标签:box only classic lag AMM not which and src
原文地址:https://www.cnblogs.com/mathlife/p/9060544.html