标签：rip   sqrt   分享   大小   说明   算法   lin   最大   www.   

TCP 拥塞控制

相关名词

1. 滑动窗口

tcp通过滑动窗口进行流量控制，所谓的窗口可以理解为接收端所能提供的缓冲区大小。

TCP是一个滑动窗口协议，即一个TCP连接的发送端在某个时刻能发多少数据是由滑动窗口控制的

1. RTT（Round trip time）

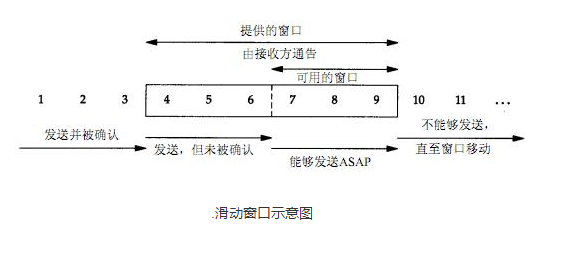
表示从发送端到接收端的一去一回需要的时间。

TCP在数据传输过程中会对RTT进行采样（即对发送的数据包及其ACK的时间差进行测量，并根据测量值更新RTT值）

1. RTO （Retransmission TimeOut）

发送数据包，启动重传定时器，重传定时器到期所花费的时间

TCP根据得到的RTT值更新RTO值，即Retransmission TimeOut，就是重传间隔，发送端对每个发出的数据包进行计时，如果在RTO时间内没有收到所发出的数据包的对应ACK，则任务数据包丢失，将重传数据。一般RTO值都比采样得到的RTT值要大。

TCP拥塞控制算法

1. BIC(Binary Increase Congestion)

2. BIC方法

• 如果发生丢包，窗口大小为W1,要保持线路满载不丢包，则说明实际窗口Wmax应该在当前窗口值W1以下。
• 如果当前窗口值W2没有丢包，则说明实际实际Wmax值应该在当前窗口值以上。

1. 何时调整？

• 每收到一个ACK时，便将窗口设置到Wmax和Wmin值的中点，直到持续接近Wmax值。

1. 如何突破？

• 当当前窗口值已经达到Wmax值时，说明带宽已经有空闲资源，此时最大带宽可能已经不止Wmax值！
• 如何去寻找新的Wmax值? 丢包! 按照逼近Wmax值的路径倒回去，采用与之对称的方案。

整个BIC过程可以参考如下图

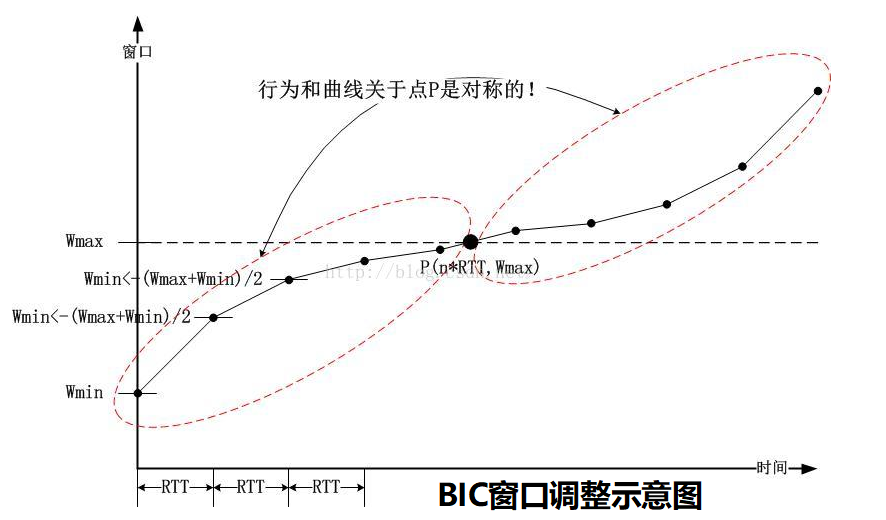
##### BIC缺陷

• 可以通过上图和下图了解到 如果RTT时间不同，通过BIC算法搜索到的Wmax的时间是不同的，因此带宽就会被RTT短的连接无情的占有。

  

?

1. CUBIC（CU-BIC?）

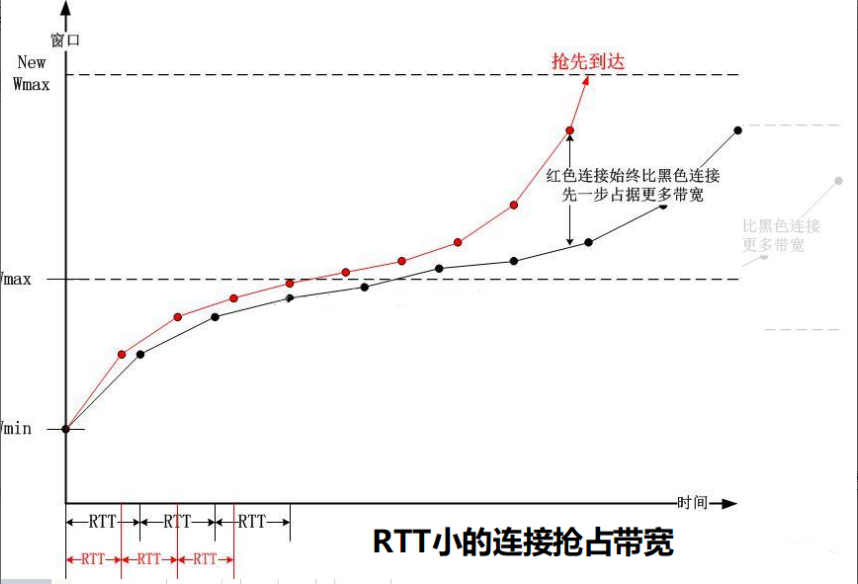
CUBIC相对于BIC解决的就是在探索Wmax的时间公平问题。

如何让寻找Wmax探索曲线跟RTT无关？

很简单。找一条数学上定义的曲线即可！该曲线的曲线方程自变量里没有RTT就好了。

Wmax曲线公示？

$f(x)=x^3-x^2+1$ 类似于BIC窗口探测曲线的公式

所以我们实际上需要确定该1元3次函数的各项参数（$f(x)=ax^3+bx^2+cx+d$）

CUBIC 公式的建立

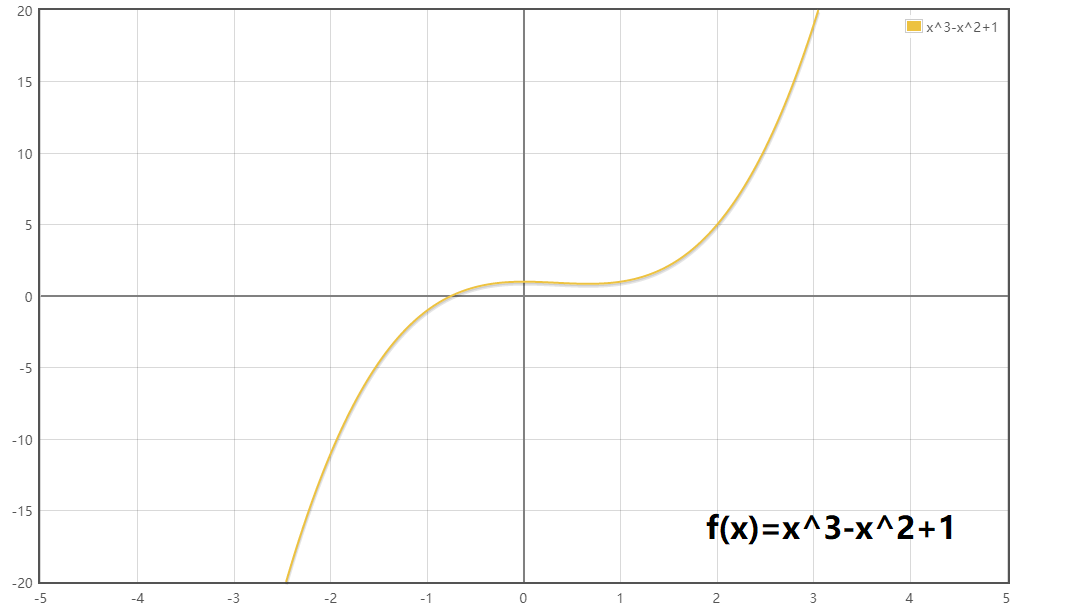
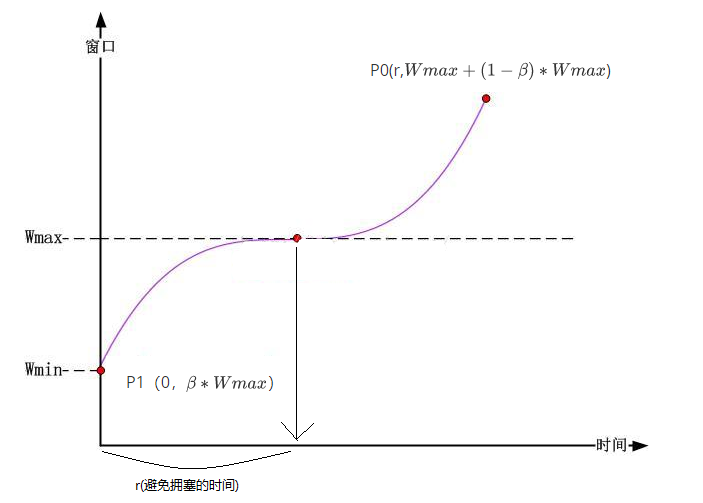
• 由上图可知 $f(x)=h(x)+Wmax$ （1）

• 其中

• $f(0)=\beta Wmax$ （2）
• $（）f（2r）=Wmax + \beta Wmax$ （3）

• $f(r)=Wmax$ （4）

• 将（2），（3），（4）代入（1）中 可得：

• $h(r)=0$ （5）

• $h(0)=(\beta-1)Wmax$ （6）

• 由实际情况我们可以合理推算出 h(x) 的一个合理形式 $h(x)=a(x-r)^3$ （7）

• 将（6）式代入到（7）中，得表达式$ r=\sqrt[3]{\frac{(1-\beta)Wmax}a} $ （8）

• 将 （7）（8）式联合代入 （1）中，并将 $a$ 替换成 c 可得 $f(x)=c(x-\sqrt[3]{\frac{(1-\beta)Wmax}a} )+Wmax$

其中 C 即 CUBIC中的C

?

CUBIC ：$f(x)=c(x-\sqrt[3]{\frac{(1-\beta)Wmax}a} )+Wmax$

到这里 我们可以理解到 $\beta$ 控制了曲线的高度，也就是 最开始的Wmin值，r则控制了从起始窗口到Wmax窗口的时间，这个r和C成反比，C越大 时间越小。

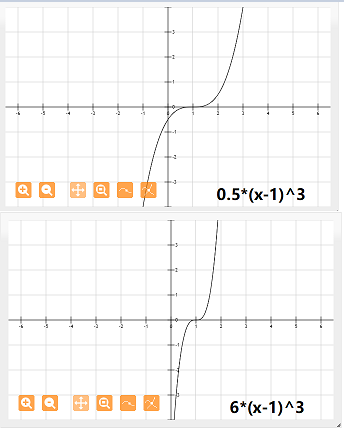
c越大，时间越小参考附图1.

因此，我们可以通过控制 C 和$\beta$的值来控制 TCP的高速率传输，而不受 RTT值的影响。

参考博客

BIC和CUBIC简介

附图一

TCP 拥塞控制

标签：rip   sqrt   分享   大小   说明   算法   lin   最大   www.   

原文地址：https://www.cnblogs.com/shitou6/p/9060423.html