标签:style blog http 使用 ar sp 2014 art c
虽然相频响应反映了系统对不同频率信号的处理时间,但并不是说相频响应越大,系统的处理时间越长。从一个简单的正弦信号exp(j*w*n)可以知道,其相位为w*n,也即是说相位不仅和时间有关,还和频率有关。在信号处理中,群延迟(Group Delay)是用来表征系统延迟时间的另外一个概念,其数学定义式如下:
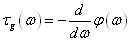
由上述定义式可以很明显地看出,群延迟更具体地表达了系统对不同频率信号的时间延迟。那么我们很自然地要问,群延迟和相频响应到底有何不同呢?
先来看一个具体的例子。假定一个信号是由两个不同频率的正弦信号叠加而成,其波形如图1 (a)所示。若将此信号通过一个反相器,即对信号乘以-1的系统,很显然反相器的相频响应是fai=pi。通过这个系统后的信号波形如图1 (b)所示。若将此信号通过一个无失真传输系统,即系统的单位冲激响应为h(n)=delta(n-n0),其中n0为常数。很显然,无失真系统的群延迟为tao=n0。通过这个系统后的信号波形如1(c)所示。对比这3个信号的波形可以看出,相比原始信号(a),通过反相器之后得到的信号(b)已经和原始信号在细节上完全不同。而通过无失真系统后的信号(c)在细节上和原始信号完全一样,只是在时间上有所延迟。
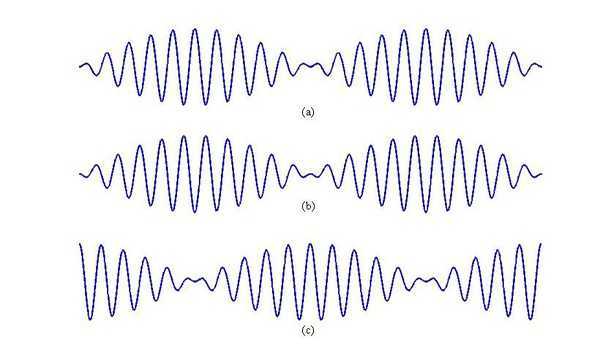
从上面的这个例子可以看出,相频响应和群延迟虽然都反映系统对不同频率信号的延迟,但两者的意义还是有所不同。相频响应反映的是系统对输入信号延迟的相对值,群延迟反映的是系统对输入信号延迟的绝对值。对于频率成分比较复杂的信号,相频响应为常数反而会造成信号的失真;群延迟为常数的系统才不会对信号产生失真。要求信号通过系统后不产生失真是很多应用场合的内在要求,比如通信信号的传输,这时候就要求系统的群延迟为常数。从群延迟的计算公式可以看出,如果群延迟为常数,则对应的相频响应有fai=-w*n0这样的形式,这也称为系统的线性相位。
在实际的信号处理当中,群延迟往往是用来衡量系统对输入信号是否产生失真,因此有的地方也称为包络延迟。而相频响应的使用则要广泛得多,这是因为一方面群延迟的计算需要用到微分,而且还需要先计算解模糊之后的相频响应,运算比较复杂;另一方面是群延迟所表示的物理意义在相频响应上也能很好地表现,比如线性相位就完全表现了群延迟为常数这种情况,这也表明相频响应是一个比群延迟内涵更宽泛的概念。
源地址:http://blog.csdn.net/deepdsp/article/details/7230815
标签:style blog http 使用 ar sp 2014 art c
原文地址:http://www.cnblogs.com/southernduck/p/3995633.html