标签:条件 str 操作 程序 for 技术分享 乘法 根据 自己的
可以理解为程序的运算步骤
n为项目的规模, 时间复杂度表示为T(n)
时间复杂度一般都为项目所有的运算步骤的渐进函数
渐进函数特征:忽略常数项
ex:
k为常数项
T(n) = n ^ 3 * k
g(n) = n ^ 3
T(n) = k * n ^ 3
g(n)就是T(n)的渐进函数
就是一个函数忽略常数项,只保留最核心,最特征的部分
1)可忽略算法增率函数的低阶项。
2)可忽略算法增率函数中高阶项的倍数常量。
3)O(f(n))+O(g(n))=O(f(n)+g(n))可组合增率函数。
分析算法时, 存在几种可能的考虑:
1. 算法完成工作最少需要多少基本操作, 即最优时间复杂度
2. 算法完成工作最多需要多少基本操作, 即最坏时间复杂度
3. 算法完成工作平均需要多少基本操作, 即平均时间复杂度
对于最优时间复杂度, 其价值不大, 因为它反映的知识最乐观最理想的情况, 没有参考价值
对于最坏时间复杂度, 提供了一种保障, 表明算法在此种程序中一定能完成工作
对于平均时间复杂度, 是对算法的一个全面评价, 因为它完整全面的反映了这个算法的性质, 但另一方面, 这种衡量并没有保障, 不是每个计算都能在这个基本操作内完成, 而且, 对于平均情况的计算, 也会因为应用算法的实例分布可能并不均匀难以计算
因此, 我们主要关注算法的最坏情况, 即最坏时间复杂度
判断一个算法的效率时,往往只需要关注操作数量的最高次项,其他次要项,常数项可以忽略不计
通常我们所讲的时间复杂度是项目的最坏时间复杂度
顺序
条件
循环
这三项可以组合所有的算法,项目
ex:
for a in range(0, n):
for b in range(0, n):
c = n - a -b
if a ^ 2 + b ^ 2 = c ^ 2:
print(a,b,c)
for a in range(0, n): (循环用乘法计算) 这句代码的运行步骤是:O(n) for b in range(0, n): (循环用乘法计算) 这句代码的运行步骤是:O(n) c = n - a -b (基本操作语句为1) 运行步骤为:O(1) if a ^ 2 + b ^ 2 = c ^ 2: print(a,b,c) 进入判断语句, 有两个分支 (当碰到分支语句的时候,取分支步骤最多的) 分支1执行print(a,b,c) 步骤为1 分支2是判断条件失败,直接跳过了 步骤为0
T(n) = O(n * n * (1+1))T(n) = O(n ^ 2 * 2)
常数项忽略: T(n) = O(n ^ 2)
扩展:
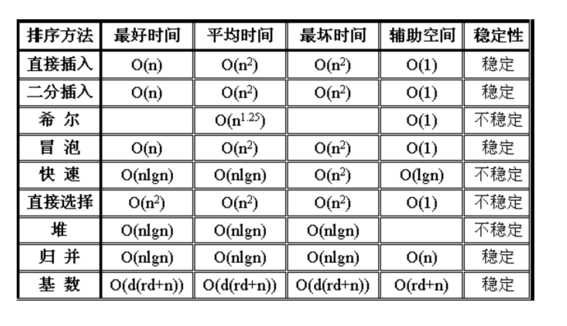
标签:条件 str 操作 程序 for 技术分享 乘法 根据 自己的
原文地址:https://www.cnblogs.com/amou/p/9073800.html