标签:有用 智商 mos ntp 思路 top 很多 final nbu
终于刷完了leetcode的前250道题的easy篇。好吧,其实也就60多道题,但是其中的套路还是值得被记录的。 至于全部code,请移步github,题目大部分采用python3,小部分使用C,如有问题和建议,欢迎指正。
有一个string库,可以返回各种string的汇总,很值得用。
当题目中需要实现字符串替代的时候,python中有一个自带的translate()函数可以实现这个功能,具体可见Python3字符串替换replace(),translate(),re.sub()
two pointers 在string题目中很常用,如前后pointers遍历整个string。
这个方法其实就是采用两个指针,分别指向string或者list或者linked list的不同位置进行遍历,其实在pythonic的解法中,这种pointer的实现方式就是数组的遍历。
eg1:141. Linked list Cycle
Given a linked list, determine if it has a cycle in it.
# Definition for singly-linked list.
# class ListNode(object):
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution(object):
def hasCycle(self, head):
"""
:type head: ListNode
:rtype: bool
"""
if head == None:
return False
runningman1 = head
runningman2 = head.next
while runningman2 != None and runningman2.next != None:
if runningman2 == runningman1 or runningman2.next == runningman1:
return True
runningman2 = runningman2.next.next
runningman1 = runningman1.next
return False这个题目是一个关于linked list的题目,此解答用了两个运动员(two pointers)的方法,一个跑的慢,一个跑的快,如果有循环,则跑的快的人一定可以追上跑的慢的人。其实解题重要的还是逻辑思路,而实现方法真的是次要的。
其实这个题目还有一种方法也很棒,具体可移步到github
eg2: 167. Two Sum II - Input array is sorted
Given an array of integers that is already sorted in ascending order, find two numbers such that they add up to a specific target number.
这个题采用的是前后two pointers的方法进行夹击:
class Solution:
def twoSum(self, numbers, target):
"""
:type numbers: List[int]
:type target: int
:rtype: List[int]
"""
i,j = 0,len(numbers)-1
while(numbers[i]+numbers[j]!=target):
if numbers[i]+numbers[j] > target:
j -= 1
else:
i += 1
return i+1,j+1eg3: 234. Palindrome Linked List
Given a singly linked list, determine if it is a palindrome.
Example: Input: 1->2->2->1 Output: true
1、这个问题可以拆解成两个问题: 一是找到该单链表的中间位置,二是反转链表
2、对于第一个问题(找到单链表的中间位置),可以通过two pointers 的方法进行,一个pointer每次走一步,另一个pointer每次走两步,当每次走两步的pointer到达final时,另一个pointer刚好在一半位置
3、对于第二个问题(反转单链表),可以标准性的分割成四个步骤:
nxt = slow.next slow.next = node node = slow slow = nxt
class Solution:
def isPalindrome(self, head):
"""
:type head: ListNode
:rtype: bool
"""
## find the mid
slow = fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
## reverse the second half
node = None
while slow:
nxt = slow.next
slow.next = node
node = slow
slow = nxt
## compare two halves
while node:
if node.val == head.val:
node = node.next
head = head.next
else:
return False
return True 其实我以前一直不知道python也可以进行位运算,直到我发现了这个题目:
eg4: 136. Single Number
Given a non-empty array of integers, every element appears twice except for one. Find that single one.
我的做法很蠢,采用的是hashmap的做法,创建一个set,然后逐个适用in运算符进行比较。其实这道题用异或(xor)是最好的方式,因为两个相同的数进行异或的二进制计算会返回全零。
求和后相减也是一个好的方法。
def singleNumber1(self, nums):
return 2*sum(set(nums))-sum(nums)
def singleNumber2(self, nums):
return reduce(lambda x, y: x ^ y, nums)
def singleNumber3(self, nums):
return reduce(operator.xor, nums)这里借用菜鸟教程里的一个图总结python里的位运算图:
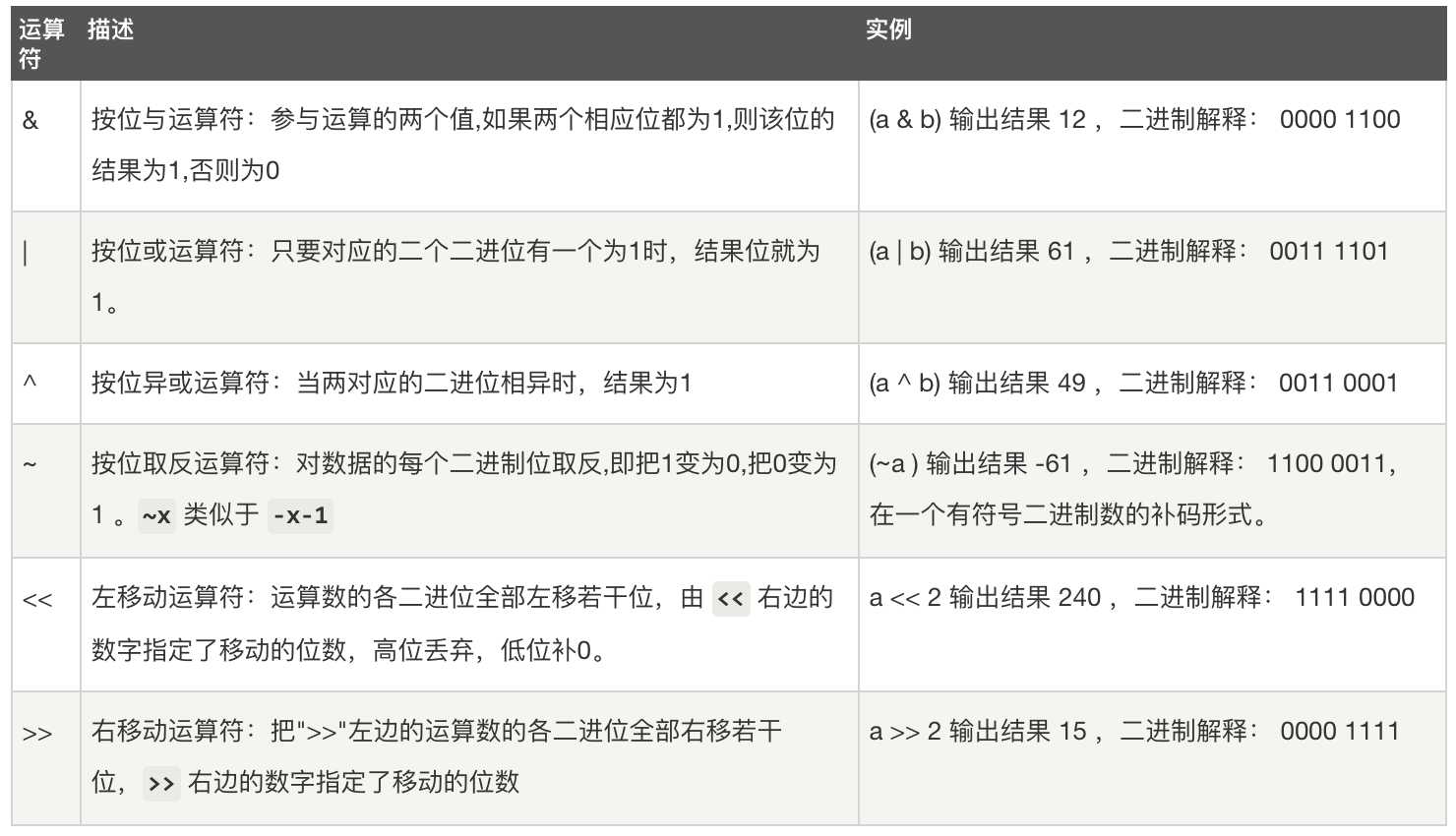
eg5: 231. Power of Two
Given an integer, write a function to determine if it is a power of two.
这个题也一样,我采用的方法如下:如果一个数为2的幂,那么他的bin形式则只有一个1,
class Solution:
def isPowerOfTwo(self, n):
"""
:type n: int
:rtype: bool
"""
if n <= 0:
return False
return bin(n).count(‘1‘) == 1还有一种更简单的方法,那就是判断n&(n-1) == 0。
note:&是位运算符。
其实对于python再说,hashtable直接用dict或者set就可以解决。
eg6: 205. Isomorphic Strings
Given two strings s and t, determine if they are isomorphic. Two strings are isomorphic if the characters in s can be replaced to get t. All occurrences of a character must be replaced with another character while preserving the order of characters. No two characters may map to the same character but a character may map to itself.
好的方法就是将s[i]和t[i]结对,然后再进行比较,使用set()即可:
def isIsomorphic(self, s, t):
return len(set(zip(s, t))) == len(set(s)) == len(set(t))实际上,这道题我采用的是用两个dict,从头遍历s和t,若元素再dict中没有则add进dict,value值为此时s或t的index,若有则判断两个dict的当前元素是否是同一个value。
然而,其实用一个dict也可以搞定:
def isIsomorphic(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
found = {}
## 这个dict的key是s[i],value值是t[i]
for i in range(len(s)):
if s[i] in found:
if not found[s[i]] == t[i]:
return False
else:
if t[i] in found.values():
return False
found[s[i]] = t[i]
return True另一种方法为使用find()函数。具体见github
eg7: 169. Majority Element
Given an array of size n, find the majority element. The majority element is the element that appears more than ? n/2 ? times. You may assume that the array is non-empty and the majority element always exist in the array.
HashMap allows us to count element occurrences efficiently.
以下是我的原始方法:
class Solution:
def majorityElement(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
countdict = {}
for num in nums:
if num not in countdict:
countdict[num] = 1
else:
countdict[num] += 1
return max(countdict.items(),key=lambda x:x[1])[0]不过,原来有一个collections.Counter()可以自动计数的啊
class Solution:
def majorityElement(self, nums):
counts = collections.Counter(nums)
return max(counts.keys(), key=counts.get)在easy的题目中,最典型的就数买股票问题了。简单来说,动态规划问题就是每次问题的处理与上一次问题处理的结果有关
eg8: 121. Best Time to Buy and Sell Stock
Say you have an array for which the ith element is the price of a given stock on day i. If you were only permitted to complete at most one transaction (i.e., buy one and sell one share of the stock), design an algorithm to find the maximum profit. Note that you cannot sell a stock before you buy one.
class Solution:
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if not prices:
return 0
else:
maxprofit = 0
minbuy = float(‘inf‘)
for p in prices:
maxprofit = max(maxprofit,p-minbuy)
minbuy = min(minbuy,p)
return maxprofiteg9: 70. Climbing Stairs
You are climbing a stair case. It takes n steps to reach to the top. Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
这也是个更典型的DP问题, 注意为了节省时间,为了不反复求解相同的子问题,可以采用1. 带备忘的自顶向下法 2. 自底向上法
下面为带备忘的方法:
class Solution:
def __init__(self):
self.demo = {}
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
if n in {1,2,3}:
return n
if n in self.demo:
return self.demo[n]
else:
value = self.climbStairs(n-1) + self.climbStairs(n-2)
self.demo[n] = value
return valueeg10: 198. House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
DP问题最重要的部分在于对于不同问题领域,最优子结构不同体现在两个方面:
1、原问题的最优解中涉及多少个子问题
2、在确定最优解使用哪些子问题时,我们需要考察多少中选择
所以,在coding之前,最好是画出问题的子问题图
对于这个例子来说,原问题需要涉及两个相邻的子问题,且只需比较demo[i]+num > demo[i+1]
class Solution:
def rob(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
if not nums:
return 0
demo = {}
demo[0] = nums[0]
demo[1] = max(nums[0:2])
for i, num in enumerate(nums[2:]):
if demo[i]+num > demo[i+1]:
value = demo[i]+num
else:
value = demo[i+1]
demo[i+2] = value
return demo[len(nums)-1]Tree的操作我喜欢用recursion,将子结点看成新的子树进行递归。
eg11: 107. Binary Tree Level Order Traversal II
Given a binary tree, return the bottom-up level order traversal of its nodes‘ values. (ie, from left to right, level by level from leaf to root).
这个问题没有用递归,而是采用queue的方式进行解答,这个也很典型。
队列中保存处理的树??的当前深度(depth)的所有结点,每deq一个结点,enq其左右子结点,当deq掉所有当前深度结点时,队列中剩下该树??下一深度所有结点。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def levelOrderBottom(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
queue = Queue()
output = []
if root:
queue.enqueue(root)
output.append([root.val])
while not queue.is_empty():
levelout = []
for _ in range(queue.size()):
node = queue.dequeue()
if node.left != None:
levelout.append(node.left.val)
queue.enqueue(node.left)
if node.right != None:
levelout.append(node.right.val)
queue.enqueue(node.right)
if levelout:
output.insert(0,levelout)
return output这道题也可以使用stack解答,只要给每一个node加一个depth的标签即可,即保存一个tuple。具体见github
eg12: 108. Convert Sorted Array to Binary Search Tree
Given an array where elements are sorted in ascending order, convert it to a height balanced BST. For this problem, a height-balanced binary tree is defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1.
对于这个题目,最适合用递归了。每次取到array的中间值,然后左右生成两个子树,依次递归。下面的代码是借用别人的回答:
def sortedArrayToBST(self, num):
if not num:
return None
mid = len(num) // 2
root = TreeNode(num[mid])
root.left = self.sortedArrayToBST(num[:mid])
root.right = self.sortedArrayToBST(num[mid+1:])
return rooteg13: 110. Balanced Binary Tree
Given a binary tree, determine if it is height-balanced. A binary tree in which the depth of the two subtrees of every node never differ by more than 1.
树??的问题通常可以用两种方法解决:
class Solution:
def isBalanced(self, root):
"""
:type root: TreeNode
:rtype: bool
"""
if not root:
return True
else:
return self.isBalanced(root.left) and self.isBalanced(root.right) and abs(self._TreeDepth(root.right)-self._TreeDepth(root.left))<=1
def _TreeDepth(self, root):
if root == None:
return 0
else:
return max(self._TreeDepth(root.left), self._TreeDepth(root.right))+1我用的第一种方法,但可以修改成如下形式,不用每次都求得每个node的深度,而是在每次求深度的过程中自动判断该node是否平衡:
class Solution(object):
def isBalanced(self, root):
def check(root):
if root is None:
return 0
## 判断左右子树是否平衡,并返回深度。若不平衡,则返回-1
leftd = check(root.left)
rightd = check(root.right)
if leftd == -1 or rightd == -1 or abs(leftd - rightd) > 1:
return -1
return 1 + max(leftd, rightd)
return check(root) != -1eg14: 112. Path Sum
Given a binary tree and a sum, determine if the tree has a root-to-leaf path such that adding up all the values along the path equals the given sum.
这道题我用的是DFS的思想,但是才baet了25%的伙伴。在看discussion的过程中,发现人的智商真是无限的。
下面的代码采用up down的形式,相当于把树??的每一层都隔绝,是一个贪心问题。
贪心算法通常都是自顶向下的设计,做出一个选择,然后求解剩下的那个子问题。
class Solution:
def hasPathSum(self, root, sum):
if not root:
return False
## 如果是叶结点
if not root.left and not root.right and root.val == sum:
return True
sum -= root.val
return self.hasPathSum(root.left, sum) or self.hasPathSum(root.right, sum)如果说leetcode的神奇之处在哪,那一定不是题目的套路,而是反套路。
eg15: 204. Count Primes
Count the number of prime numbers less than a non-negative number, n.
要求比一个数n小的所有质数的数量,那么就排除掉所有不是质数的数。
怎么排除呢?如果一个数是非质数,那么这个数一定是所有<sqrt(n)的数中某一个数的倍数。
class Solution:
def countPrimes(self, n):
"""
:type n: int
:rtype: int
"""
if n < 3:
return 0
primes = [True] * n
primes[0] = primes[1] = False
for i in range(2, int(n**0.5)+1):
primes[i*2::i] = [False] * len(primes[i*2::i])
return sum(primes)eg16: 189. Rotate Array
Given an array, rotate the array to the right by k steps, where k is non-negative.
Example: Input: [1,2,3,4,5,6,7] and k = 3 Output: [5,6,7,1,2,3,4] Explanation: rotate 1 steps to the right: [7,1,2,3,4,5,6] rotate 2 steps to the right: [6,7,1,2,3,4,5] rotate 3 steps to the right: [5,6,7,1,2,3,4]
这道题很多种解法,用python的话最容易的解法应该属于slice直接替换,但是每一次slice都会产生一个额外的copy,从而消耗了空间。
其实这道题就简单直白的一个个元素依次往前替换就可以了,这样可以只消耗O(1)的空间。
class Solution:
def rotate(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: void Do not return anything, modify nums in-place instead.
"""
if k !=0 and k!=len(nums):
k = k % len(nums)
count = len(nums)
start = 0
while count>1:
current = (start + k) % len(nums)
while current != start:
temp = nums[current]
nums[current] = nums[start]
nums[start] = temp
current = (current + k) % len(nums)
count -= 1
start += 1
count -= 1eg17: 172. Factorial Trailing Zeroes
Given an integer n, return the number of trailing zeroes in n!. Example: Input: 3 Output: 0 Explanation: 3! = 6, no trailing zero.
这是一道数学题,是一道考智商的题目。我真的没有这么聪明想出好的办法,可以有人想得出啊! 这里引用别人的一番话:
Because all trailing 0 is from factors 5 * 2. But sometimes one number may have several 5 factors, for example, 25 have two 5 factors, 125 have three 5 factors. In the n! operation, factors 2 is always ample. So we just count how many 5 factors in all number from 1 to n.
所以说,这个题目所有的0都是由于5提供的。所以每隔5个数有一个5,每隔55个数有两个5,每隔55*5个数有3个5...
class Solution:
def trailingZeroes(self, n):
"""
:type n: int
:rtype: int
"""
return 0 if n == 0 else n // 5 + self.trailingZeroes(n // 5)Reference:
标签:有用 智商 mos ntp 思路 top 很多 final nbu
原文地址:https://www.cnblogs.com/bjwu/p/9085178.html