标签：分享   处理   开始   enter   一段   lca   模拟   之间   image   

树链剖分入门讲解

问题导入

    当我们做题目的时候，往往会有一些题目是给定一颗树，并对这颗树做一堆蛇皮怪物般的操作的。

    比如：
    1.询问x到y路径上的最小最大最￥#%￥#@￥@#￥值
    2.询问x到y路径上的xor，和，乘@！#￥@#￥%￥#值
    3.纯模拟是过不了的且往往与lca挂钩
    4.没有动态的加边删边23333
    5.往往下面还要接一个线段树

那么，我们要怎么做呢？

这里提供一种思想，就是把树拆掉，以轻重边为基础的拆边，把一颗树拆成大大小小的几条链放到类似于常用的线段树里面加以操作。

轻重边

在树链剖分里，我们定义如下规则

1.重儿子:当前节点的儿子节点中子树大小最大的那一个
2.轻儿子:当前节点除了重儿子以外的所有儿子节点

那么

重链即为重儿子连成的链，轻链即为轻儿子连成的链。

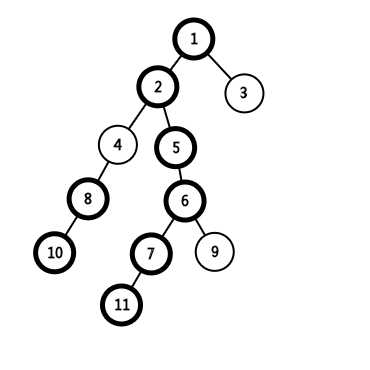
我们可以通过这张图看到如下分链解释

节点1的儿子（2,3）中2的子树大小更大所以选取2为重儿子。
节点6的儿子（7,9）中7的子树大小更大所以选取7为重儿子。

但是并不是轻儿子后面就一定是一直是轻链的，比如节点4后面就又接了一条重链。
我们可以这样理解，当一个节点选取了一个重儿子以后，它其他的轻儿子节点就重新开始，按照之前的规则选择它的轻重儿子。

我们可以观察到，重链上的任意两点之间的路径是不是都在这条重链上，可以化成链直接在线段树上调用了。

且还有如下两个性质

    1.轻边(u,v)中, size(u)≤ size(u/2)
    2.从根到某一点的路径上,不超过logn条轻链和不超过logn条重链。
    （蒟蒻表示并不会证）

其实我们在这里还能发现如果要统计一个点的轻重儿子，是不是还能顺便处理出它的子树size。
那么我们要怎么处理出重儿子和轻儿子呢？DFS序。

DFS序

（以下内容引至洛谷讲义）

    我们DFS一棵树的时候,对这棵树的每个点按照访问的时间进行重标号,就得到了树的DFS序列。 这个序列可以有效地处理一些树上的问题。 如图就是一棵树的一种可能的DFS序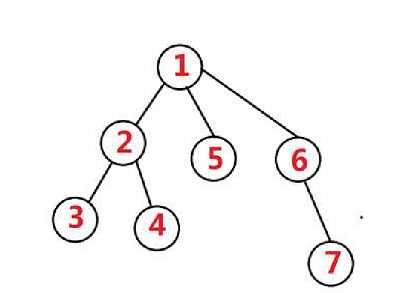

    记录DFS的时候每个点访问起始时间与结束时间,记最起始时间是前序遍历,结束时间是后序遍历。可以发现树的一棵子树在DFS序上是连续的一段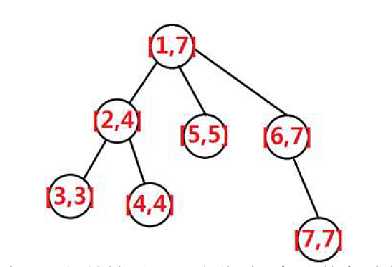

    如图, DFS之后,那么树的每个节点就具有了区间的性质。那么此时,每个节点对应了一个区间,而且可以看到,每个节点对应的区间正好“管辖”了它子树所有节点的区间,那么对点或子树的操作就转化为了对区间的操作。

等几天再填坑。。。。蛙蛙蛙蛙（咕咕咕咕咕）

树链剖分讲解

标签：分享   处理   开始   enter   一段   lca   模拟   之间   image   

原文地址：https://www.cnblogs.com/hhh1109/p/9085447.html