标签:cstring max 技术 #define 建图 source 枚举 cst size
题意是让我们找出所有的这样的图形:
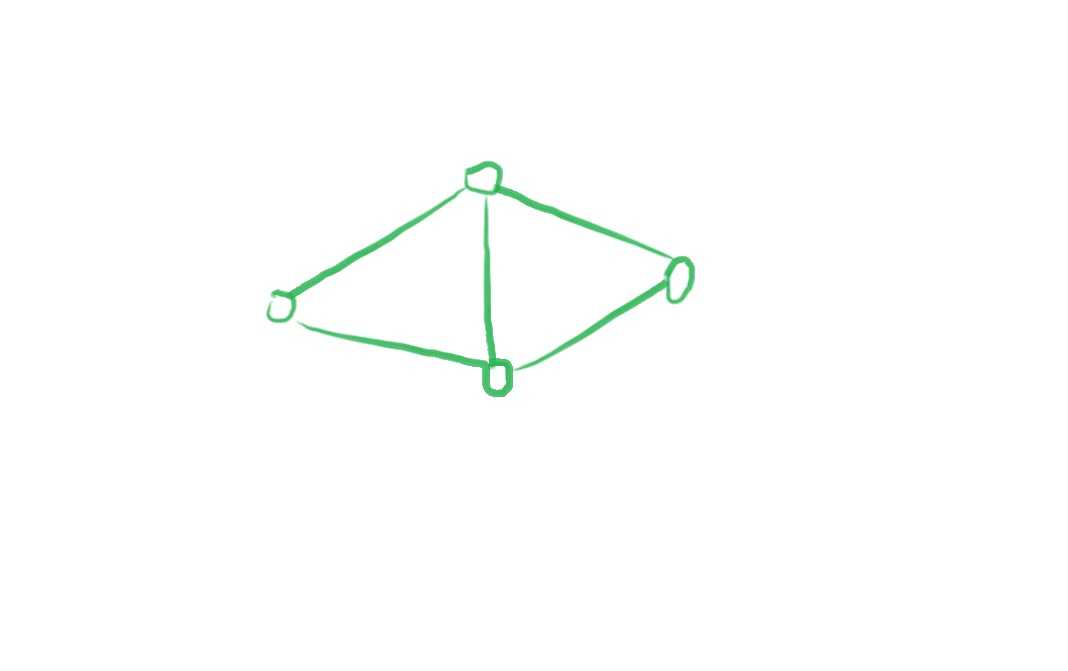
我们只需要求出每条边分别在多少个三元环中,记为\(x\),再然后以该点为中心的图形数就是\({x \choose 2}\)
所以我们只需找出所有三元环
据说这是一个套路题
我们将所有无向边改为有向边,由度数小的向度数大的连边,度数相同就由编号小的向编号大的
容易发现这样建图一定是一个\(DAG\)
然后我们枚举边,将边的两端点出边的到达的点打上标记,当一个点被打上同一个标记时,就成环了
因为是\(DAG\)容易发现这样找环不会重复
然后就是时间复杂度证明
是\(O(m\sqrt{m})\)的
我们只需证明每个点出度不大于\(\sqrt{m}\)
假设有一个点出度大于\(\sqrt{m}\),那么由建边方式我们至知道出边到达的点度数不比该点小,这样总的边数就大于\(m\)了,不符
所以点的度数是\(O(\sqrt{m})\)的
为什么在\(hdu\)使用\(pair\)会\(CE\) = =
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<utility>
#define Redge(u) for (int k = h[u]; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define mp(a,b) (node){a,b}
#define cls(s) memset(s,0,sizeof(s))
#define cp node
#define LL long long int
using namespace std;
const int maxn = 100005,maxm = 200005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == ‘-‘) flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
struct node{
int first,second;
};
int h[maxn],ne;
struct EDGE{int to,nxt,id;}ed[maxm];
inline void build(int u,int v,int x){
ed[++ne] = (EDGE){v,h[u],x}; h[u] = ne;
}
int de[maxn],a[maxm],b[maxm],now,n,m,ans[maxm];
cp vis[maxn];
int main(){
while (~scanf("%d%d",&n,&m)){
ne = now = 0;
REP(i,n) vis[i] = mp(0,0),h[i] = de[i] = 0;
REP(i,m){
ans[i] = 0;
a[i] = read(); b[i] = read();
de[a[i]]++; de[b[i]]++;
}
REP(i,m){
if (de[a[i]] > de[b[i]] || (de[a[i]] == de[b[i]] && a[i] > b[i]))
swap(a[i],b[i]);
build(a[i],b[i],i);
}
REP(i,m){
now++;
Redge(a[i]) vis[ed[k].to] = mp(now,ed[k].id);
Redge(b[i]) if (vis[ed[k].to].first == now){
ans[i]++;
ans[ed[k].id]++;
ans[vis[ed[k].to].second]++;
}
}
LL ret = 0;
REP(i,m) if (ans[i] > 1) ret += ans[i] * (ans[i] - 1) / 2;
printf("%lld\n",ret);
}
return 0;
}hdu6184 Counting Stars 【三元环计数】
标签:cstring max 技术 #define 建图 source 枚举 cst size
原文地址:https://www.cnblogs.com/Mychael/p/9090006.html