NP难问题

标签：不能   nbsp   时间复杂度   com   问题   sdn   定义   SM   tail   

摘自网址https://blog.csdn.net/u014295667/article/details/47090639

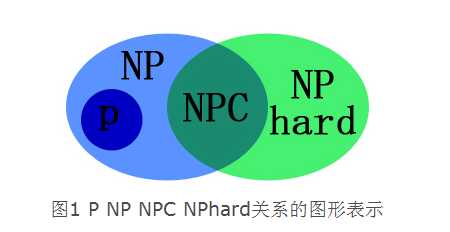
P类问题：在多项式时间内可解的问题。

NP类问题（Nondeterminism Polynomial）：在多项式时间内“可验证”的问题。也就是说，不能判定这个问题到底有没有解，而是猜出一个解来在多项式时间内证明这个解是否正确。

NPC类问题（Nondeterminism Polynomial complete）：存在这样一个NP问题，所有的NP问题都可以约化成它。换句话说，只要解决了这个问题，那么所有的NP问题都解决了。其定义要满足2个条件： 

• 首先，它得是一个NP问题；
• 然后，所有的NP问题都可以约化到它。

要证明npc问题的思路就是： 

• 先证明它至少是一个NP问题，
• 再证明其中一个已知的NPC问题能约化到它。

NP难问题  即多项式复杂程度的非确定性问题。它满足NPC问题定义的第二条但不一定要满足第一条（就是说，NP-Hard问题要比 
NPC问题的范围广，NP-Hard问题没有限定属于NP），即所有的NP问题都能约化到它，但是他不一定是一个NP问题。NP-Hard问题同样难以找到多项式的算法，但它不列入我们的研究范围，因为它不一定是NP问题。即使NPC问题发现了多项式级的算法，NP-Hard问题有可能仍然无法得到多项式级的算法。事实上，由于NP-Hard放宽了限定条件，它将有可能比所有的NPC问题的时间复杂度更高从而更难以解决。

NP难问题

标签：不能   nbsp   时间复杂度   com   问题   sdn   定义   SM   tail   

原文地址：https://www.cnblogs.com/vinn/p/9095856.html