标签:向量 迭代 相对 9.png 等于 旋转矩阵 python 建立 之间
最近几个月因为工作接触到了机械臂的项目,突然对机械臂运动方法产生了兴趣,也就是如何控制机械臂的位置和姿态。借用一张网上的图片,应该是ur5的尺寸。我用到的是ur3机械臂,除了尺寸不一样,各关节结构和初始位置和ur5是一样的。
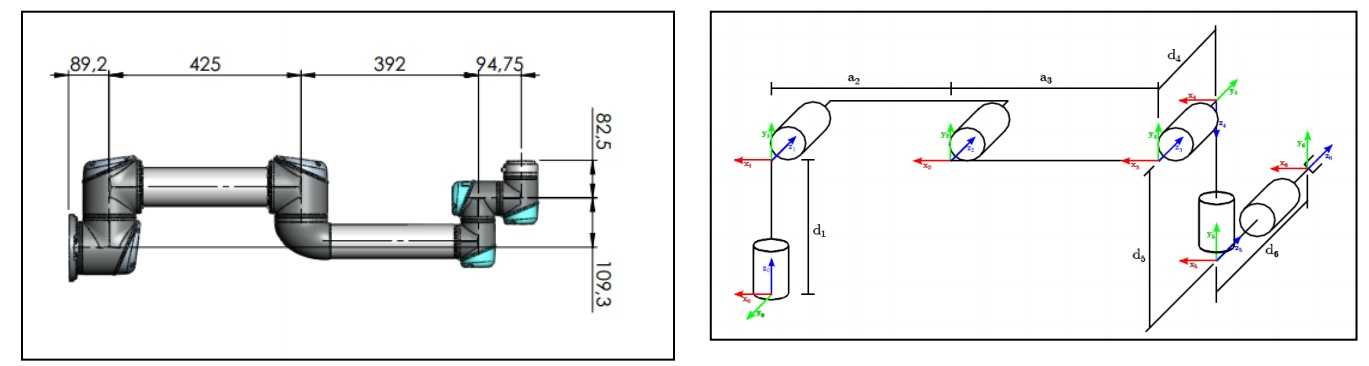
ur机械臂是六自由度机械臂,由D-H参数法确定它的运动学模型,连杆坐标系的建立如上图所示。我当时在这个地方的理解上走了不少弯路,后来找个一个视频,我觉得讲解地比较容易理解,可以参考一下Denavit-Hartenberg参数视频详解。ur机械臂DH参数表如下,
转动关节θi是关节变量,连杆偏移di是常数。
|
关节编号 |
α(绕x轴) |
a(沿x轴) |
θ(绕z轴) |
d(沿z轴) |
|
1 |
α1=90 |
0 |
θ1 |
d1=89.2 |
|
2 |
0 |
a2=-425 |
θ2 |
0 |
|
3 |
0 |
a3=-392 |
θ3 |
0 |
|
4 |
α4=90 |
0 |
θ4 |
d4=109.3 |
|
5 |
α5=-90 |
0 |
θ5 |
d5=94.75 |
|
6 |
0 |
0 |
θ6 |
d6=82.5 |
由此可以建立坐标系i在坐标系i-1的齐次变换矩阵,注意每次不管平移还是旋转是相对于当前的运动坐标系变换,矩阵右乘

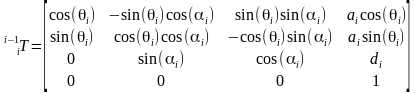
那么把DH参数代入就可以得到所有相邻坐标系的变换矩阵
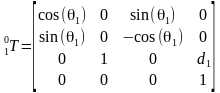
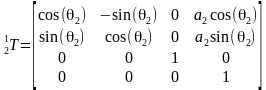
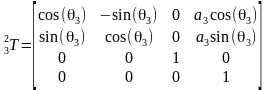
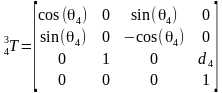
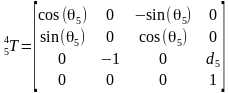
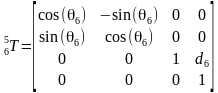
所以末端坐标系6到基座固定坐标系0的变换矩阵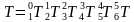 。那么求正解就很简单了,只要输入六个关节角度θi,就得到末端坐标在基坐标系的变换矩阵T。ur机械臂的视教板上末端点的坐标是用六个值[x, y, z, rx, ry, rz]表示的。前三个值[x, y, z]是三维笛卡尔坐标,表示空间位置,后三个值[rx, ry, rz]是坐标旋转向量,表示空间姿态。我们得到的变换矩阵T怎么变成六值坐标[x, y, z, rx, ry, rz]呢?设
。那么求正解就很简单了,只要输入六个关节角度θi,就得到末端坐标在基坐标系的变换矩阵T。ur机械臂的视教板上末端点的坐标是用六个值[x, y, z, rx, ry, rz]表示的。前三个值[x, y, z]是三维笛卡尔坐标,表示空间位置,后三个值[rx, ry, rz]是坐标旋转向量,表示空间姿态。我们得到的变换矩阵T怎么变成六值坐标[x, y, z, rx, ry, rz]呢?设
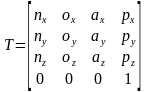
T的左上角的3x3矩阵是旋转矩阵,旋转矩阵和旋转向量之间可以通过罗德里格斯(Rodrigues)变换进行转换。opencv里有相应的函数调用。算法也比较简单,不用opencv的函数自己写代码也不难。T的右上角3x1就是空间位置[x, y, z]。这样有变换矩阵T得到六值坐标,完成了正解。
逆解相对要复杂一些,由末端的空间位置和姿态,计算可能的关节角度。逆解的方法有解析法,迭代法和几何法。其中解析法用数学推导,可以得到全部根,但是计算复杂。有的机械臂可以得到无穷解,比如7轴机械臂。而ur的6轴机械臂是有有限解的。这里推导一下ur的逆解。
首先计算求变换矩阵T过程其中的一些中间矩阵。
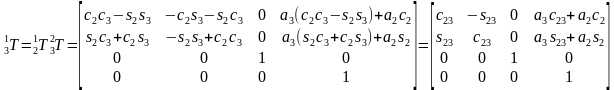 ,其中c23=cos(θ2+θ3),s23=sin(θ2+θ3)。
,其中c23=cos(θ2+θ3),s23=sin(θ2+θ3)。
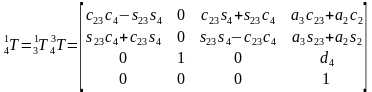
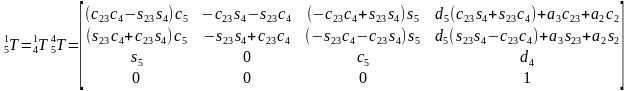
由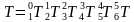 得到
得到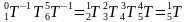 。计算
。计算
 ,
, ,得到
,得到
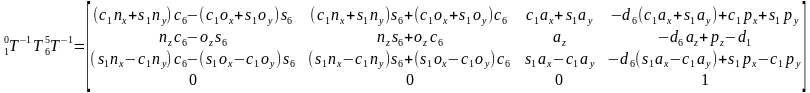
等式两边矩阵的行列应该分别相等,由第三行第四列得到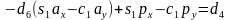 ,可解得
,可解得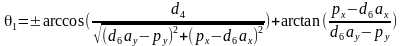 ,有两个解。这里注意写程序的时候,求解这里的反正切是用atan2()这类的函数,返回之在(-π,+π]。而反余弦的返回值在[0,π],从而保证在2π范围每个解是唯一的。
,有两个解。这里注意写程序的时候,求解这里的反正切是用atan2()这类的函数,返回之在(-π,+π]。而反余弦的返回值在[0,π],从而保证在2π范围每个解是唯一的。
由第三行第三列得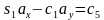 ,可解得
,可解得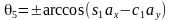 ,两个解。由第三行第二列得到
,两个解。由第三行第二列得到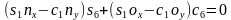 ,可解得
,可解得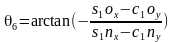 。
。
接着由
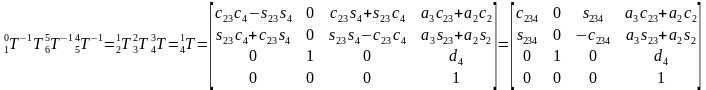 ,
,
计算
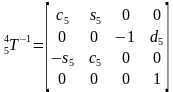 ,得出等式左边等于
,得出等式左边等于
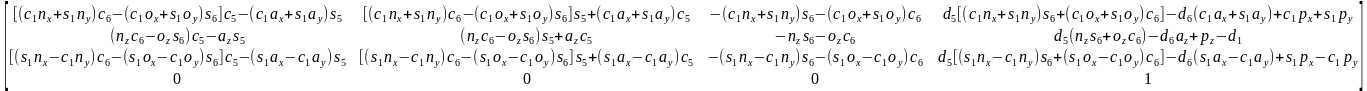 。
。
由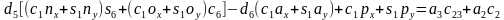 ,两边平方,令
,两边平方,令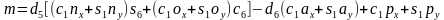 ,
,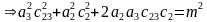 。
。
同样由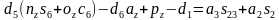 ,令
,令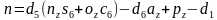 ,
,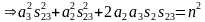 。
。
两式相加得到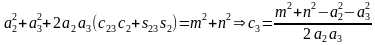 ,则
,则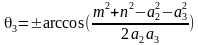 ,有两个解。
,有两个解。
把θ3带入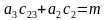 和
和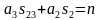 ,得
,得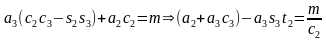 ,
,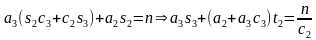 ,其中t2=tanθ2。两式消去c2,得到
,其中t2=tanθ2。两式消去c2,得到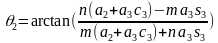 。
。
最后得到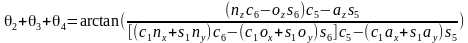 ,从而得到θ4。
,从而得到θ4。
综合有两个解的情况,ur机械臂逆解总共由2x2x2=8组解。
按照上面的算法,用python写了两个程序,一个正解一个逆解验证一下。工作手边是ur3的机械臂,上面的图和表都是ur5的,换成ur3的参数。正解算出来都没有问题,可以和实际机械臂的空间位姿对应。可是逆解算出来8组值,好像只有四组值是对的。一直还没理解到底是怎么回事,仔细检查了算法和程序好像都没有错阿,不知道是哪里出了问题。网上也没有找到答案,如果哪位大神知道,望不吝赐教!
标签:向量 迭代 相对 9.png 等于 旋转矩阵 python 建立 之间
原文地址:https://www.cnblogs.com/mightycode/p/9095059.html