标签:use define msu loss tom 微软 思考 就是 相关
这一部分比较基础,没有太多视觉相关的。。
假定在著名的 CIFAR10数据集上,包含10类数据。每类数据有10000条?
目标是输入一个图片,通过模型给出一个label。线性回归的思想就是
 得到到F(x)作为某个类别的分数。那么针对每个可能的label都经过一个线性函数输出一个分值,那么我们选最大的其实就是最有可能的分数。
得到到F(x)作为某个类别的分数。那么针对每个可能的label都经过一个线性函数输出一个分值,那么我们选最大的其实就是最有可能的分数。
为什么这么做是合理的?
角度1:
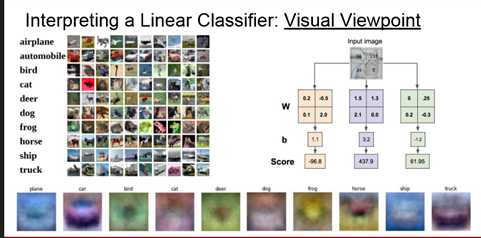
每个种类一个 template,每个线性函数的W的训练过程就类似于上图中得到的底部那些图片的过程。比如horse这个种类得到的W,看起来就好像有了2个头,其实就是训练的过程中综合了horse这类图像,然后越和这个图像相似,得分就越高。
角度2:
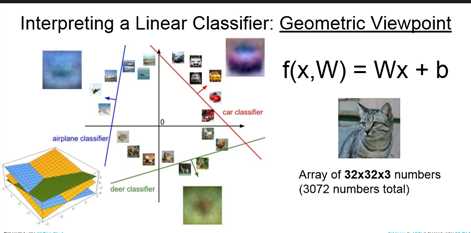
一堆线性函数将整个空间进行了划分,得到每一类。
角度3:
代数的观点,计算得分。
这段比较迷,从线性回归直接到svm的多分类。。讲的很好理解。自己以前却看了很久。。。
我们知道给了一个模型,能得到一个结果。那么怎么评测这个结果到底好不好呢?
引出了损失函数(用来计算一个得分,通过输入)。比如我们一直讨论的 CIFAR10数据集,我们在用上面的线性回归给出了不同种类的分数,那么怎么评价这些分数的好坏呢?
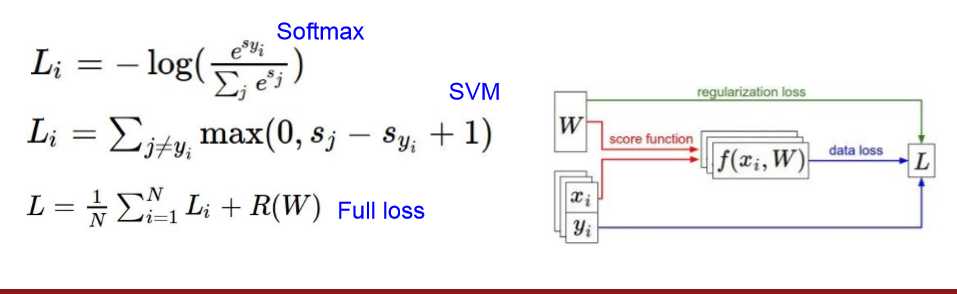
这里采用了合页损失(hinge-loss),也就是 。假定对于第i个样本,真实的label用
。假定对于第i个样本,真实的label用 表示,经过线性函数得到的分数用S表示,在某个类别下的分数用
表示,经过线性函数得到的分数用S表示,在某个类别下的分数用 表示,那么关于样本i的损失可以写作
表示,那么关于样本i的损失可以写作
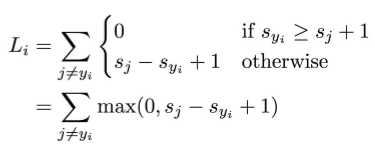
也就是 的时候损失为0.效果最高。
的时候损失为0.效果最高。
接着几个小问题加深了对这个损失函数的理解。
Q: What happens to loss if car scores change a bit?
因为当正确的分数比其他的分数 要高出一个delta(这里是1)损失才为0,那么有微小的变化没影响。
Q2: what is the min/max possible loss?
当我们完全的分对。损失为0,最差正无穷。
Q3: At initialization W is small so all s ≈ 0. What is the loss?
C-1
Q4: What if the sum was over all classes? (including j = y_i)
多算了j本身这项,损失函数多了1.
Q5: What if we used mean instead of sum?
没影响
Q6: What if we used
加重了损失。
接着引出了正则化!
如果w使得损失函数为0,那么这个w是不是唯一的?
显然不是,2w得到的损失函数也是0.
那么选择哪个好?
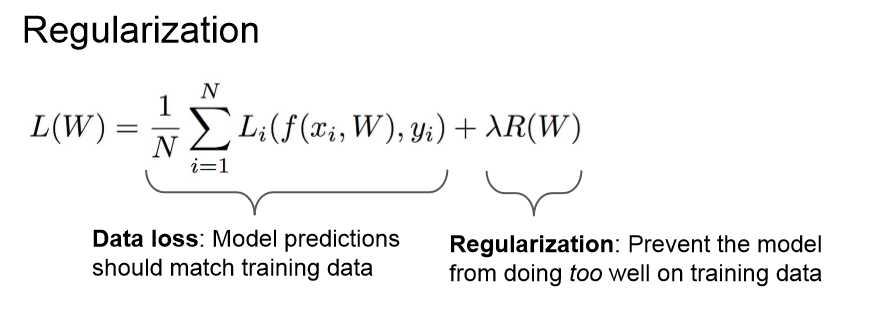
前半部分是训练数据上的损失,后面是对于参数w的惩罚,防止过拟合。这里的lambda是个超参数,在惩罚与拟合数据之间进行平衡。
最常用的正则化方法!


 也就是2个范数间平衡
也就是2个范数间平衡Why regularize?

 (也就是对正确的概率取了对数,加了负号。)
(也就是对正确的概率取了对数,加了负号。)
小思考:
Q: What is the min/max possible loss L_i?
A: min 0, max infinity
Q2: At initialization all s will be approximately equal; what is the loss?
A: log(C), eg log(10) ≈ 2.3 这一点可以用来再第一步的时候测试自己代码是不是正确
以线性回归作为引子,逐步拉出来了分类svm,正则化方法,softmax回归。多元svm和softmax区别主要是 softmax的损失函数的优化过程一直想要更好的结果。然而svm多分类只要达到一定程度是没有区别的。比如[10,2,2],[10,-2,-2]这2种得分。多元svm认为这2种效果一样。然而softmax则认为第二种更好,并且想着继续优化。
标签:use define msu loss tom 微软 思考 就是 相关
原文地址:https://www.cnblogs.com/cbfstudy/p/9102877.html