标签:info 回归 时序 img 分布 通过 数值 管理 不同
指数追踪,利用某些金融资产组合去追踪某一股票指数,指数型基金核心技术。 目前主要有两种指数复制方法 基于两种假设 一:历史能够重演,在过去一段时间能构造历史追踪误差最小的,未来也将是最优,现在大多数指数复制类型为此类。二:从统计角度,找到与目标指数具有最大相关 具有协整关系的股票组合,保证未来表现与未来尽可能一致。
从股票数量复制角度,分为两种,完全复制和不完全复制,完全复制按照指数构造方式购买成分证券,但市场时序上变化迅速,造成成本高,逐渐不被使用。不完全复制根据优化方法寻找成分证券及其投资权重。
先引入模型变量
:
模型的构建:

至此,我们就可以得到了如下的一个回归问题
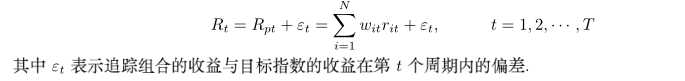
w(it)表示第i支股票t时刻的权重,如果将其处理为与时间有关的,则此线性回归问题将变得非常复杂,难以处理,为对此优化,我们采用固定比率策略,即w(it)=w(i)。这样有两个好处,一,从策略角度,为一个追涨杀跌策略,保证组合的流动性。二,模型简化为一个二次规划问题,能够很容易的求解。
至此,将指数追踪转为了一个多元线性回归问题。
传统线性回归方法为最小二乘回归,将损失函数选择为均方误差:
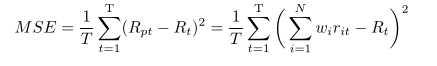 (*)
(*)
(*)式表示了学习过程的经验风险,传统理论认为,经验风险最小,即模型未来预测能力越强,但现在考虑过拟合情况,使用传统机器学习中的svm,其具有较好泛化能力,采用结构风险最小策略,即参数量越少越好,同时参数越接近0越好,重新定义我们的损失函数:
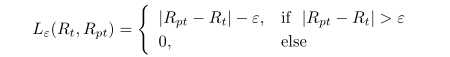
其中ε为松弛变量,是一个接近于0但大于0的数,它的大小控制了svm中支持向量的个数,为一个超参数,需要人手工设计。
现在我们的目标函数即为:
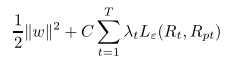
最小化第一项,代表最小化结构风险,同时能代表svm中的间隔最大化,即有最好的预测能力;最小化第二项表示最小化经验损失,其中 λ为不同时期的经验损失的权重,金融中,越接近现在的,认为其含有较多未来信息,需要对现在的经验损失提高权重,为此我们采用基于指数加权方式来计算 λ
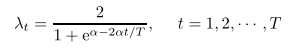
其中α同样为一个超参数,需要人为设计,再次,我们设定为1。
至此我们的目标函数已经建立起来,接下来,就是对约束条件的讨论:
自然有的两个边界为资本预算以及投资比例:
![]()
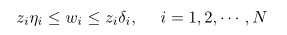
从管理方面需要考虑股票的数目,数目越大,管理成本和难度越大,同样选取一个超参数k,其代表投资组合内最大股票种类
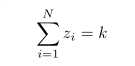
同时限制 z 为0 1变量,为0即不进入组合,为1即进入组合。
以上讨论了约束条件和目标函数,最终我们得到了我们的指数复制模型:
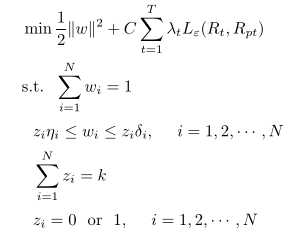
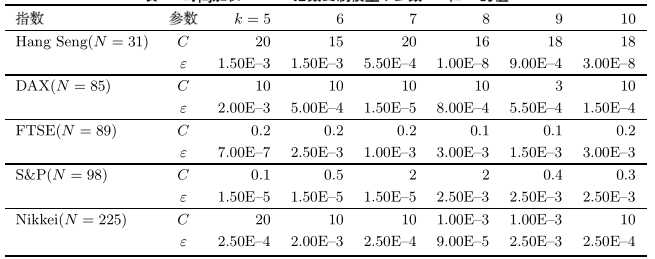
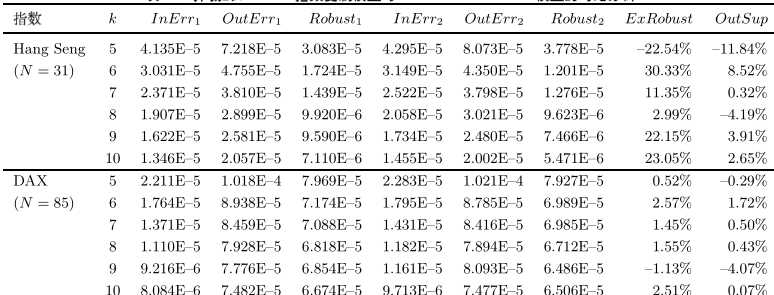
从鲁棒性和样本外追踪效果来看,优于Ruiz-Torrubiano模型
一,借助于svm中松弛变量以及支持向量的思想,进一步提高了模型泛化性能;
二,时间加权,更加准确
想法:
1 svm中更为强大的是核技巧,怎么将核函数应用于其中,去更好的提高泛化能力
2 模型中有几个需要人为去指定和设计的超参数,依赖于人的经验,如何去智能调参,可能参考现在深度学习的重要方向 元学习 对其的经验损失中的超参数 怎么类比到深度学习中的正则化项
3指数复制中一个重要问题为基金按模型执行策略时,自身参加到了市场中,自己也对市场产生了影响,如同得到了解析解,但实际计算数值解时,发现其数据有噪声,导致数值解不稳定,最终成为了一个不适当问题,如何将这种行为考虑进入模型中,可以参考一下我之前讲解的GNN的思想,通过寻找稳定解去解决一部分问题
4不同时期,市场有着不同风格,可以认为数据不是同种分布,而机器学习模型都假设数据有着同一分布,可以将市场分割为不同周期,每个周期有着不同的参数,以往数据更多是去验证模型的优越性,而模型参数更多依赖于近期数据。
以上就是我对徐凤敏教授《基于时间加权svm指数复制模型和实证分析》的浅解,期望做她的研究生,做更深一步的研究!!
标签:info 回归 时序 img 分布 通过 数值 管理 不同
原文地址:https://www.cnblogs.com/shenliao/p/9104433.html