标签:ide spl hid 时间复杂度 角度 div display 分享 iostream
传送门:https://www.luogu.org/problemnew/show/P1119

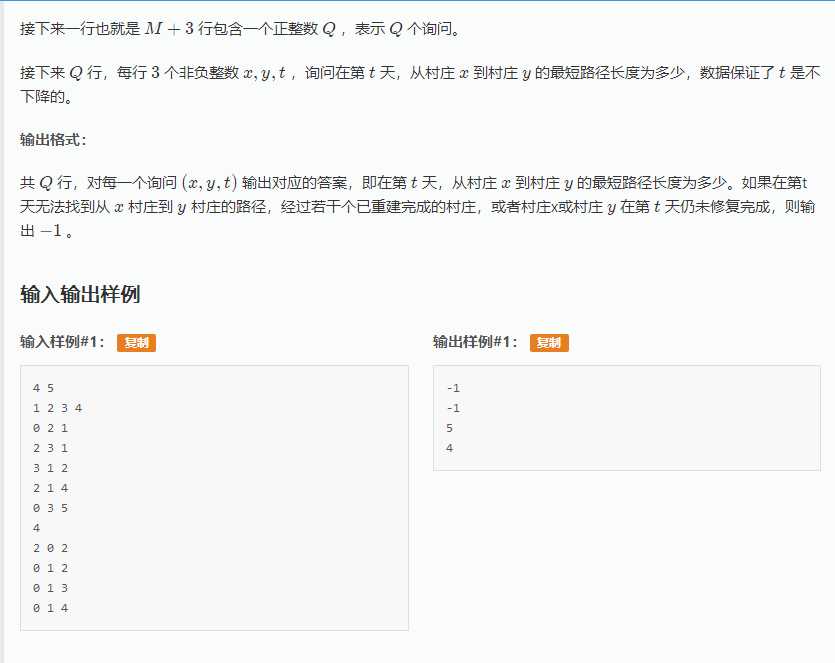

这题的思想很巧妙.
首先,我们可以考虑一下最暴力的做法,对每个时刻的所有点都求一遍单元最短路
因为最多只有200个时刻,时间复杂度为O(n^3log(n+m))) (堆优化的迪杰斯特拉)
显然对于n=200,并过不了
我们可有进一步分析
这一题,我们堆优化的迪杰斯特拉慢在每加入一个点,我们每一次都得对全图彻彻底底做一轮松弛
那换个角度考虑,如果我只松弛经过新加入的点的点对呢?
没错,就得用Floyd了.
因为Floyd本质就是一个DP,给了我们极大的魔改的空间
考虑到Floyd最外层循环就是枚举加入的点,我们就可以只枚举里面那两层枚举点对的循环.
也就是说我们只用考虑它有可能松弛到的点.
当然,在此之前,我们得先把这个点有关的边先连回去
然后先用两层循环(枚举中转点和起始点)来松弛终点为加入点的路径
接下来用刚刚说的两层循环来松弛经过新加入点路径就好
时间复杂度O(n^3)
然后就OjbK了
具体请看代码

//Luogu P1119 灾后重建 //May,28th,2018 //巧妙的floyed松弛 #include<iostream> #include<cstdio> #include<cstring> using namespace std; const int N=200+10; long long read() { long long x=0,f=1; char c=getchar(); while(!isdigit(c)){if(c==‘-‘) f=-1;c=getchar();} while(isdigit(c)){x=x*10+c-‘0‘;c=getchar();} return x*f; } int n,m,T[N],dis[N][N],e[N][N]; int main() { n=read(),m=read(); memset(T,0x3f,sizeof T); memset(dis,0x3f,sizeof dis); memset(e,0x3f,sizeof e); for(int i=0;i<n;i++) T[i]=read(); for(int i=1;i<=m;i++) { int a=read(),b=read(),temp=read(); e[a][b]=e[b][a]=temp; } for(int i=0;i<n;i++) e[i][i]=dis[i][i]=0; int Q=read(),to=0; for(int i=1;i<=Q;i++) { int x=read(),y=read(),t=read(); while(T[to]<=t) { for(int j=0;T[j]<=t;j++) dis[to][j]=dis[j][to]=min(dis[to][j],e[to][j]); for(int j=0;T[j]<=t;j++) for(int k=0;T[k]<=t;k++) dis[to][k]=dis[k][to]=min(dis[k][to],dis[k][j]+dis[j][to]); for(int j=0;T[j]<=t;j++) for(int k=0;T[k]<=t;k++) dis[j][k]=min(dis[j][k],dis[j][to]+dis[to][k]); to++; } if(dis[x][y]==0x3f3f3f3f) printf("-1\n"); else printf("%d\n",dis[x][y]); } return 0; }
标签:ide spl hid 时间复杂度 角度 div display 分享 iostream
原文地址:https://www.cnblogs.com/GoldenPotato/p/9105731.html