标签：style blog http color io os 使用 ar for
开学以后各种堕落，刷题的时间都用来不知道干啥去了，难得打一场cf啊。
第一场正儿八经参加的cf，题目貌似很水不过我弱就不想解释别的啥了。
AC了A,B,D三题：
A没啥好说的吧
code:
1 #include <cstdio> 2 #include <iostream> 3 #include <cstdlib> 4 #include <cstring> 5 #include <algorithm> 6 using namespace std; 7 int a[10]; 8 int cnt[10]; 9 int main(){ 10 bool q=0; 11 int num=0; 12 memset(cnt,0,sizeof(cnt)); 13 for (int i=1;i<=6;i++){ 14 scanf("%d",&a[i]); 15 cnt[a[i]]++; 16 } 17 for (int i=1;i<=9;i++){ 18 if (cnt[i]>=4) {q=1;cnt[i]-=4;} 19 } 20 for (int i=1;i<=9;i++){ 21 if (cnt[i]!=0) num++; 22 } 23 if (q==0) printf("Alien\n"); 24 else { 25 if (num==1) printf("Elephant\n"); 26 else printf("Bear\n"); 27 } 28 return 0; 29 }
B，也是够水不过自己编码能力太差写了接近200行的代码。。。。。。
1 #include <cstdio> 2 #include <cstdlib> 3 #include <cstring> 4 #include <vector> 5 #define pb push_back 6 using namespace std; 7 int n; 8 vector <int> que[2020]; 9 int main(){ 10 scanf("%d",&n); 11 for (int i=1;i<=n;i++){ 12 int x; 13 scanf("%d",&x); 14 que[x].pb(i); 15 } 16 int t=1; 17 for (int i=1;i<=2000;i++){ 18 int l=que[i].size(); 19 if (l>0) t=t*l;if (t>=3) break; 20 } 21 if (t<3) {printf("NO\n");return 0;} 22 printf("YES\n"); 23 bool q=0; 24 int k,t1,t2,t3; 25 for (int i=1;i<=2000;i++){ 26 if (que[i].size()>=3) { 27 q=1;k=i;t1=que[i][0];t2=que[i][1];t3=que[i][2];break; 28 } 29 } 30 if (q) { 31 int last=0; 32 for (int i=1;i<=2000;i++){ 33 if (i==k) { 34 printf("%d %d %d",t1,t2,t3);last+=3; 35 if (last!=n) printf(" "); 36 for (int j=3;j<que[i].size();j++){ 37 printf("%d",que[i][j]); 38 last++; if (last!=n) printf(" "); 39 } 40 }else 41 for (int j=0;j<que[i].size();j++) { 42 printf("%d",que[i][j]); 43 last++; if (last!=n) printf(" "); 44 } 45 } 46 printf("\n"); 47 last=0; 48 for (int i=1;i<=2000;i++){ 49 if (i==k) { 50 printf("%d %d %d",t1,t3,t2);last+=3; 51 if (last!=n) printf(" "); 52 for (int j=3;j<que[i].size();j++){ 53 printf("%d",que[i][j]); 54 last++; if (last!=n) printf(" "); 55 } 56 }else 57 for (int j=0;j<que[i].size();j++) { 58 printf("%d",que[i][j]); 59 last++; if (last!=n) printf(" "); 60 } 61 } 62 printf("\n"); 63 last=0; 64 for (int i=1;i<=2000;i++){ 65 if (i==k) { 66 printf("%d %d %d",t2,t1,t3);last+=3; 67 if (last!=n) printf(" "); 68 for (int j=3;j<que[i].size();j++){ 69 printf("%d",que[i][j]); 70 last++; if (last!=n) printf(" "); 71 } 72 }else 73 for (int j=0;j<que[i].size();j++) { 74 printf("%d",que[i][j]); 75 last++; if (last!=n) printf(" "); 76 } 77 } 78 printf("\n"); 79 }else { 80 int k1,k2,t1,t2,t3,t4; 81 k1=0;k2=0; 82 for (int i=1;i<=2000;i++){ 83 if (que[i].size()==2) if (k1==0) { 84 k1=i;t1=que[i][0];t2=que[i][1]; 85 }else { 86 k2=i;t3=que[i][0];t4=que[i][1]; 87 break; 88 } 89 } 90 int last=0; 91 for (int i=1;i<=2000;i++){ 92 if (i==k1) { 93 printf("%d %d",t2,t1); 94 last+=2; 95 if (last!=n) printf(" "); 96 for (int j=2;j<que[i].size();j++) 97 { 98 printf("%d",que[i][j]); 99 last+=1; 100 if (last!=n) printf(" "); 101 } 102 } 103 if (i==k2) { 104 printf("%d %d",t3,t4); 105 last+=2; 106 if (last!=n) printf(" "); 107 for (int j=2;j<que[i].size();j++) 108 { 109 printf("%d",que[i][j]); 110 last+=1; 111 if (last!=n) printf(" "); 112 } 113 } 114 if (i!=k1 && i!=k2) { 115 for (int j=0;j<que[i].size();j++){ 116 printf("%d",que[i][j]); 117 last++; 118 if (last!=n) printf(" "); 119 } 120 } 121 } 122 printf("\n"); 123 for (int i=1;i<=2000;i++){ 124 if (i==k1) { 125 printf("%d %d",t1,t2); 126 last+=2; 127 if (last!=n) printf(" "); 128 for (int j=2;j<que[i].size();j++) 129 { 130 printf("%d",que[i][j]); 131 last+=1; 132 if (last!=n) printf(" "); 133 } 134 } 135 if (i==k2) { 136 printf("%d %d",t3,t4); 137 last+=2; 138 if (last!=n) printf(" "); 139 for (int j=2;j<que[i].size();j++) 140 { 141 printf("%d",que[i][j]); 142 last+=1; 143 if (last!=n) printf(" "); 144 } 145 } 146 if (i!=k1 && i!=k2) { 147 for (int j=0;j<que[i].size();j++){ 148 printf("%d",que[i][j]); 149 last++; 150 if (last!=n) printf(" "); 151 } 152 } 153 } 154 printf("\n"); 155 last=0; 156 for (int i=1;i<=2000;i++){ 157 if (i==k1) { 158 printf("%d %d",t1,t2); 159 last+=2; 160 if (last!=n) printf(" "); 161 for (int j=2;j<que[i].size();j++) 162 { 163 printf("%d",que[i][j]); 164 last+=1; 165 if (last!=n) printf(" "); 166 } 167 } 168 if (i==k2) { 169 printf("%d %d",t4,t3); 170 last+=2; 171 if (last!=n) printf(" "); 172 for (int j=2;j<que[i].size();j++) 173 { 174 printf("%d",que[i][j]); 175 last+=1; 176 if (last!=n) printf(" "); 177 } 178 } 179 if (i!=k1 && i!=k2) { 180 for (int j=0;j<que[i].size();j++){ 181 printf("%d",que[i][j]); 182 last++; 183 if (last!=n) printf(" "); 184 } 185 } 186 } 187 printf("\n"); 188 } 189 return 0; 190 }
C等会儿再说吧。
D:
明显地是差分之后模式匹配，匹配可以用KMP算法，Hash(Rabin-Karp)，如果有闲情逸致就去写suffix array吧。
问题是KMP。。。我这个渣渣已经一年多没写过了。。。电脑上没有现成模板，但好在对算法本身还是记得很清楚的，于是凭感觉写了个效率有点低的KMP
好在一个小时之后终于把它给憋出来了。。变量名都很取得很别扭。
1 #include <cstdio> 2 #include <cstring> 3 #include <cstdlib> 4 using namespace std; 5 int n,m; 6 int a[200001],b[200001]; 7 int x[200001],y[200001]; 8 int next[200001]; 9 int main(){ 10 scanf("%d%d",&n,&m); 11 for (int i=1;i<=n;i++){scanf("%d",&a[i]);} 12 for (int i=1;i<n;i++) {x[i]=a[i+1]-a[i];} 13 for (int i=1;i<=m;i++){scanf("%d",&b[i]);} 14 for (int i=1;i<m;i++) {y[i]=b[i+1]-b[i];} 15 if (m==1) {printf("%d\n",n);return 0;} 16 n--;m--; 17 memset(next,0,sizeof(next)); 18 int pos=2,pre=1; 19 while (pos<=m){ 20 while (y[pre]==y[pos] && pos<=m) { 21 next[pos]=pre;pos++;pre++; 22 } 23 if (pos<=m) { 24 pre=next[pre-1]+1;if (pre==1) { 25 if (y[pre]!=y[pos]) { 26 next[pos]=0;pos++; 27 } 28 } 29 } 30 } 31 int p1=1,p2=1,ans=0; 32 while (p1<=n) { 33 if (p2==1 && y[p2]!=x[p1]) p1++; 34 while (y[p2]==x[p1]) { 35 if (p2==m) {ans++;p2=next[p2];} 36 p2++;p1++; 37 if (p1>n) break; 38 } 39 if (p1>n) break; 40 if (p2<=m) {p2=next[p2-1]+1;} 41 42 } 43 printf("%d\n",ans); 44 return 0; 45 }
现在来看C吧，C这题先是看英文看得很不爽，（其实看下图就明白了。。。）后来感觉它让我想起了URAL1017：
http://acm.timus.ru/problem.aspx?space=1&num=1017
那题我用背包做的。。。这里N<=10^12肯定挂，又想到还要可能还要高精，洗洗睡吧。
题解是这么写的（全文翻译，锻炼英文吧）
Card house. This problem required some maths, but just a little bit. So in order to start here let‘s first observe that the number of cards you need to use for a complete floor with R rooms equals to:
C = Crooms + Cceiling = 2·R + (R - 1) = 3·R - 1
Then if you have F floors with Ri rooms on the i-th floor then the total number of cards would be:
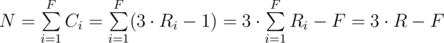
where R is the total number of the rooms in the card house.
This already gives you an important property — if you divide N + F on 3 then the remainder of this division should be 0. This means that if you have found some minimum value of floors somehow and you found maximum possible number of floors in the house, then within that interval only every third number will be a part of the solution, the rest of the numbers will give a non-zero remainder in the equation above.
Now let‘s think what is the highest house we can build using N cards. In order to build the highest possible house obviously you need to put as few cards on each floor as you can. But we have a restriction that every floor should have less rooms than the floor below. This gives us the following strategy to maximize the height of the house: we put 1 room on the top floor, then 2 rooms on the floor below, then 3 rooms on the next floor, etc. In total then the number of cards we will need equals to:
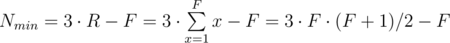
This is minimum number of cards we need in order to build a house with F floors. This gives us a way to calculate the maximum height of the house we can build using N cards, we just need to find maximum F which gives Nmin < = N. Mathematicians would probably solve the quadratic inequation, programmers have two options:
Check all possible F until you hit that upper bound. Since Nmin grows quadratically with F then you will need to check only up to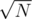 
numbers. This gives 
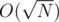time complexity and fits nicely in the given time limit.
The second approach would be a binary search. Using binary search to find maximum number of the floors would give you O(logN)time complexity. This was the intended originally solution but it was decided to lower the constraints in order to allow sqrt solutions as well.
Now that you know the maximum number of the floors in the house you might need to correct it a bit because of that remainder thing we discussed above, this might make your maximum height one or two floors lower. Looking again at the remainder discussion on top we can see that starting from here only every third number will be valid for an answer. Now you can either count them brutally (back to 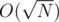solution) or you can simply calculate them using this formulae:
ans = (Fmax + 3 - 1) / 3 (integer division)
That seems to be it, just don‘t forget to use longs all the time in this problem.
Card House:这个问题需要一点数学，但只是很少的一点数学，所以开始我们先观察如果要建完整的有R个房间的一层需要多少张卡片。
C=3R-1
所以如果你有F层，第i层有Ri张卡片，那么总共需要的卡片数=3R-F
其中R=Sigma(Ri)
这已经给了你一个重要性质 ———用N+F除三的余数一定是0， 这意味着如果你找到了可能的F的最大值和最小值， 那么在那个范围中只有每间隔三个的可能为解, 其它的数都会产生不为0的余数。
现在我们来考虑我们用N张卡片能够搭的最高的房子，为了搭建最高的房子很显然我们需要在每层放尽可能少的卡片，但我们有一个限制就是每层的房间数必须小于下层。这给了我们一个策略来使层数最大，我们令顶层有1个房间，第二层有两间，第三层有三间，以此类推， 卡片的总数等于：
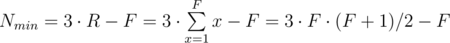
这是我们建F层房屋需要的最少的卡片数N，这给了我们一种方式计算n张卡片能够建的房屋的最大层数，我们只需找到最大的 F 使得 Nmin < = N. 数学家们可能会去解这个二次不等式，程序员有一下两种方式：
检验所有可能的F 直到达到上界. 因为 Nmin与 F 是二次关系所以你最多会检验 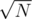个数字. 其时间复杂度为 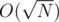而且完美地符合了本题的时限。
第二种方式是二分查找. 用二分查找计算F的最大值的时间复杂度为 O(logN). 这是原来的解法，但为了使开方级别的算法也能通过本题的数据规模降低了。
现在你知道了房屋的层数的最大值，你可能需要稍微检验一下它因为上面讨论过的问题,这可能让你的最大层数少1到2行.从上面的讨论可以发现从这里开始只有每三个数满足要求. 现在你可以暴力计算它们 (回到 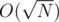的解法) 或者简单地用下面的公式计算
ans = (Fmax + 3 - 1) / 3 (整除)
这就是全部，只是不要忘记在整个过程中都应该使用长整型。
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
什么？？原来我把题目看错了当成了计数（论学好英文的重要性）。。。好吧，那么也不存在什么高精的问题了，直接做吧，也是水题。
1 #include <iostream> 2 using namespace std; 3 long long n,fM; 4 int main(){ 5 cin>>n; 6 for (fM=1;3*fM*(fM+1)/2-fM<=n;fM++);fM--; 7 while ((n+fM)%3!=0) fM--; 8 cout<<(fM+2)/3<<endl; 9 return 0; 10 }
至于E嘛，我觉得还是等AC的人多一点的时候再做做吧
标签：style blog http color io os 使用 ar for
原文地址：http://www.cnblogs.com/yzh119/p/3997370.html
