标签:data- fill TE 基本 The 一个 odi 等于 math
由逻辑回归的基本原理,我们将客户违约的概率表示为p,则正常的概率为1-p。因此,可以得到: 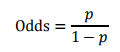
此时,客户违约的概率p可表示为: 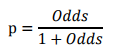
评分卡设定的分值刻度可以通过将分值表示为比率对数的线性表达式来定义,即可表示为下式: 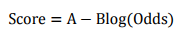
其中,A和B是常数。式中的负号可以使得违约概率越低,得分越高。通常情况下,这是分值的理想变动方向,即高分值代表低风险,低分值代表高风险。
逻辑回归模型计算比率如下所示: 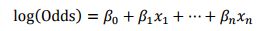
其中,用建模参数拟合模型可以得到模型参数β0,β1,…,βn。β0,β1,…,βn。
式中的常数A、B的值可以通过将两个已知或假设的分值带入计算得到。通常情况下,需要设定两个假设:
(1)给某个特定的比率设定特定的预期分值;
(2)确定比率翻番的分数(PDO)
根据以上的分析,我们首先假设比率为x的特定点的分值为P。则比率为2x的点的分值应该为P+PDO。代入式中,可以得到如下两个等式: 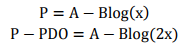
假设 设定评分卡刻度使得比率为{1:20}(违约正常比)时的分值为50分,PDO为10分,代入式中求得:B=14.43,A=6.78
则分值的计算公式可表示为: 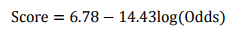
评分卡刻度参数A和B确定以后,就可以计算比率和违约概率,以及对应的分值了。通常将常数A称为补偿,常数B称为刻度。
则评分卡的分值可表达为: 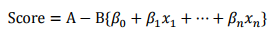
式中:变量x1…xnx1…xn是出现在最终模型中的自变量,即为入模指标。由于此时所有变量都用WOE转换进行了转换,可以将这些自变量中的每一个都写(βiωij)δij(βiωij)δij的形式: 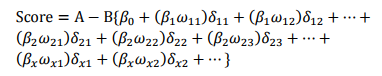
式中ωijωij 为第i行第j个变量的WOE,为已知变量;βiβi为逻辑回归方程中的系数,为已知变量;δijδij为二元变量,表示变量i是否取第j个值。上式可重新表示为:
此式即为最终评分卡公式。如果x1…xnx1…xn变量取不同行并计算其WOE值,式中表示的标准评分卡格式,如表3.20所示:
表3.20表明,变量x1有k1行,变量x2有k2行x1有k1行,变量x2有k2行,以此类推;基础分值等于(A?Bβ0)(A?Bβ0);由于分值分配公式中的负号,模型参数β0,β1,…,βnβ0,β1,…,βn也应该是负值;变量xixi的第j行的分值取决于以下三个数值:
(1)刻度因子B;
(2)逻辑回归方程的参数βiβi;
(3)该行的WOE值,ωijωij
标签:data- fill TE 基本 The 一个 odi 等于 math
原文地址:https://www.cnblogs.com/nick477931661/p/9117725.html