标签:style blog http color io ar for 数据 sp
http://acm.hdu.edu.cn/showproblem.php?pid=5047
题目大意:
给n条样子像“m”的折线,求它们能把二维平面分成的面最多是多少。
解题思路:
我们发现直线1条:2平面;2直线:4平面;3直线:7平面......因为第n条直线要与前面n-1条直线都相交,才能使分的平面最多,则添加第n条直线,平面增加n个;
所以公式是面F = 2 + 2 + 3 + ......+ n = (1+n)*n/2 + 1
因为题目的是“M”的折线,一个“M”有4条线将平面分成2块,4条直线将平面分成11块,它们之间相差9块; 当两个“M”,平面分成19块,8条直线,平面分成37块,相差18,
是9的倍数。平面每增加一个“M”,平面的相当于增加4条直线,但要减去9块(结论在徒弟百度上面找到的,我也不知道为什么)。这个结论适合"z",“V”....这些折线都适合。
给n个“M”,公式F = (1+4*n)*4*n/2+1-n*9 = n*(8*n-7)+1
因为n最大是10^12,__int64(long long)都是9*10^18,n*n就会数据溢出。开始的时候没有计算时间复杂度,就用普通的大数运算,结果超时。后来师兄说大数有优化,
就是将一个大数分成左右两部分,分别用__int64 存。
因为防止两个数相乘数据溢出,所以我的数右半部分是9位数。举个例子 2100123456789,ans1=2100,ans0=123456789;
因为这个大数这样分,最多两部分所以推到公式如下
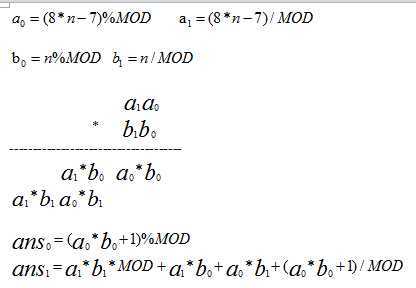
AC代码:
1 #include<cstdio> 2 3 typedef __int64 LL; 4 5 #define MOD 1000000000 6 7 int main(){ 8 LL n, a[2], b[2], ans[2]; 9 int t; 10 scanf("%d", &t); 11 for(int cs = 1; cs <= t; ++cs){ 12 scanf("%I64d", &n); 13 14 a[0] = (8 * n - 7) % MOD; 15 a[1] = (8 * n - 7) / MOD; 16 17 b[1] = n / MOD; 18 b[0] = n % MOD; 19 20 ans[0] = a[0] * b[0] + 1; 21 ans[1] = a[1] * b[0] + a[0] * b[1] + a[1] * b[1] * MOD + ans[0] / MOD; 22 ans[0] %= MOD; 23 24 printf("Case #%d: ", cs); 25 if(ans[1]){ 26 printf("%I64d%09I64d\n", ans[1], ans[0]); 27 }else{ 28 printf("%I64d\n", ans[0]); 29 } 30 } 31 return 0; 32 }
,
标签:style blog http color io ar for 数据 sp
原文地址:http://www.cnblogs.com/xuqiulin/p/3997589.html