标签:制造 oid mes http 初始 sdn class for lse
一:状压dp的基本特征
状态压缩问题一般是指用十进制的数来表示二进制下的状态
这种用一个数来表示一组数,以降低表示状态所需的维数的解题手段,就叫做状态压缩。
常用到位运算
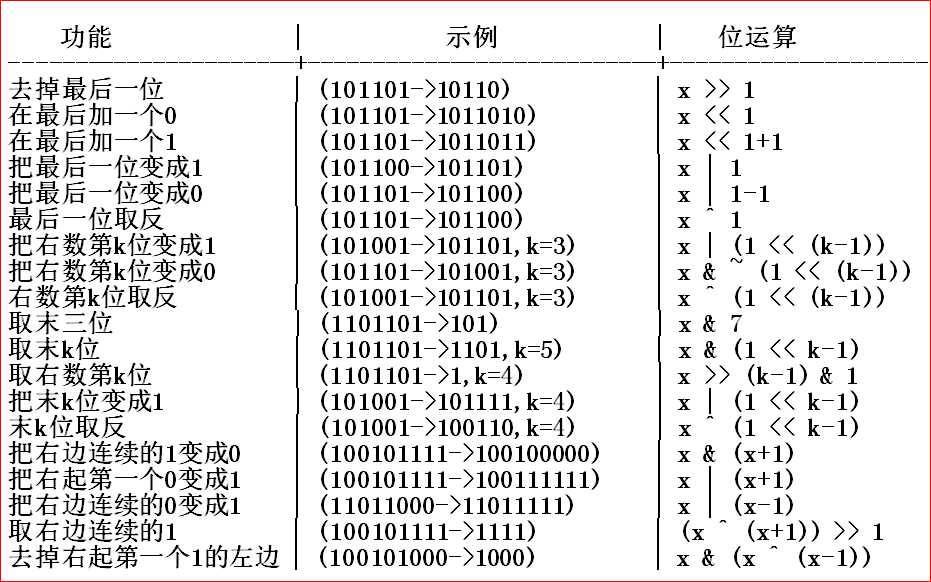
二:位运算
&:与运算,相同为1不同为0
| :或运算,全0位0,否则为1
^:异或运算,不同为1,相同为0(也叫半加与运算)
<<:左移操作,x<<j,x在二进制下向左移j位,(也就是原来的数乘j即:x*=j)右边用0填充,反码不同,要用1填充(负数)
>>:右移操作,x>>j相当于x=/j,左边反码,补码补1(负数)
例:
1.判断一个数字x在二进制下的第i位是不是为1if(((i<<(i-1))&x)>0)
将1左移i-1位,相当于制造了一个只有第i位为1其他位都是0的二进制数,然后用该数与x做与运算
2.把一个数字x在二进制下的第x为更改为1
x|=(1<<(i-1))
eg:
有一个n*m的棋盘(1<=n<=5,1<=m<=1000)现有1*2和2*1的小木块无数
要想盖满整个棋盘有多少种方法,答案大于1000000007,mod1000000007。
#include <cstdio> #include <cstring> #include <algorithm> #include <iostream> using namespace std; int N, M; //n,m分别代表棋盘的长宽 long long dp[1005][34]; //dp[i][j]表示对于前i-1行,第i行采用第j(一个十进制的数)种状态时,得到的方案可行的总数 void dfs(int i,int j,int state,int nex) //这里i代表列数,j代表当前位数(也可以说是行数-1,初始时为0),state代表状态数,nex代表下一列出现的状态 { if (j==N) //用if判断每种情况都尝试去做,而不用if...else判断 { dp[i+1][nex]+=dp[i][state]; return; } if (((1<<j)&state)>0) dfs(i,j+1,state,nex); //如果这个位置已经被上一列所占用,直接跳过 if (((1<<j)&state)==0) dfs(i,j+1,state,nex|(1<<j)); //如果这个位置是空的,尝试放一个左右覆盖1*2的木板 if (j+1<N && ((1<<j)&state)==0 && ((1<<(j+1))&state)==0) dfs(i,j+2,state,nex); //如果这个位置以及下一个位置都是空的,尝试放一个上下覆盖2*1的木板,而此时要跳过下一个木块 return; } int main() { while (cin>>N>>M) { memset(dp,0,sizeof(dp)); dp[1][0]=1; //初始化第一列状态为0的方法数等于1 for (int i=1;i<=M;i++) //外层for循环遍历每一列 { for (int j=0;j<(1<<N);j++) //内层for遍历每一个列的所有状态 if (dp[i][j]) //只要dp[i][j]方法数不为空,就执行dfs方法 { dfs(i,0,j,0); } } cout<<dp[M+1][0]<<endl; //最后dp[m+1][0]就是结果 } }
https://blog.csdn.net/harrypoirot/article/details/23163485
一个大佬讲的状压dp
标签:制造 oid mes http 初始 sdn class for lse
原文地址:https://www.cnblogs.com/tianzeng/p/9127490.html