标签:about ota time problem target contain immediate rom cpp
Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.
A k-tree is an infinite rooted tree where:
The picture below shows a part of a 3-tree.
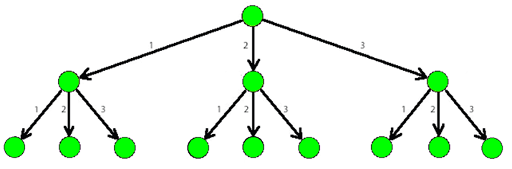
Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (109?+?7).
A single line contains three space-separated integers: n, k and d (1?≤?n,?k?≤?100; 1?≤?d?≤?k).
Print a single integer — the answer to the problem modulo 1000000007 (109?+?7).
3 3 2
3
3 3 3
1
4 3 2
6
4 5 2
7
#include <iostream>
#include<bits/stdc++.h>
using namespace std;
const int modd=1e9+7;
int main()
{
int n,k,d;
cin>>n>>k>>d;
long long dp[2][105];
memset(dp,0,sizeof(dp));
dp[0][0]=1;
dp[1][0]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=k;j++)
{
if(i<j)break;
dp[0][i]=(dp[0][i]+dp[0][i-j])%modd;
}
for(int j=1;j<=d-1;j++)
{
if(i<j)break;
dp[1][i]=(dp[1][i]+dp[1][i-j])%modd;
}
}
cout<<((dp[0][n]-dp[1][n])%modd+modd)%modd;//这里加了两个odd是因为要保证结果为正数
return 0;
}
code forces431C_dp_注意结果要多加两个modd保证输出是正数
标签:about ota time problem target contain immediate rom cpp
原文地址:https://www.cnblogs.com/passion-sky/p/9139171.html