2.逻辑回归关于二分类问题的理解

标签：span   回归   一个   似然函数   strong   两种   构建   nbsp   表示   

1.问题引入

总括：逻辑回归其实就是将分类问题数学化，也就是将类别的现象用具体的函数去刻画。

现象：如下图，就是一个二分类的具体现象，我们总可以找到一条曲线（判定边界）将两种现象或者特征分割开来.

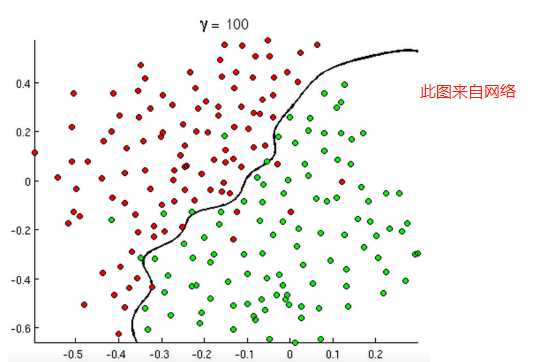
2.问题求解

问题1：如何用函数去刻画上述分类问题中的判定边界？

　　我们可以将上述判定边界分成两个类别，线性与非线性；

　　　　1).线性判定边界方程如下：

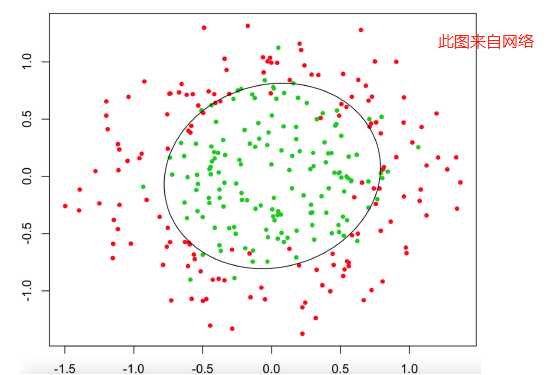
　　　　2).非线性判定边界：

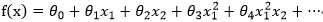
问题2：有了边界方程，我们如何刻画分类现象呢？

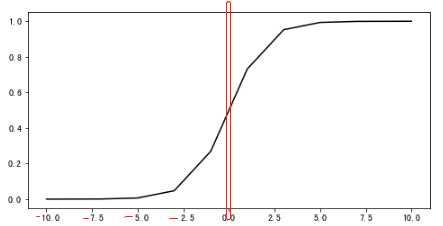
　　1).二分类问题，其实可以理解为一个非此即彼的问题，对于此类问题我们就可以考虑看是否能够转化成一个概率问题，此处我们引入sigmoid函数；

　　　　函数表达式为：

　　　　图像：当z<0时，函数值小于0.5，当z>0时函数值大于0.5

　　　　我们以问题引入中的图为例，我们在两类特征中各取一个点代入判定边界方程，必然会得到符号相反的两个数，再结合sigmoid函数我们便可以将二分类刻画为g(z)>0.5的为一类，g(z)<0.5的为一类

　　　　方程为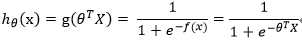：，其中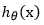表示样本点x关于θ的函数

　　2).构建概率模型刻画分类问题

　　　　我们可以将y=1定义为一个类别，将y=0定义成为另外一个类别

　　　　下式（1），我们就将y=1这个类别的概率p定义为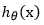，我们知道对于非此即彼的问题概率之和永远为1，那y=0这个类别的概率，自然为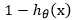

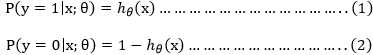
　　　　将上式整合便可表示为：

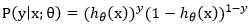
　　　　到此我们已经完成类将一个二分类的现象转化为数学中实际的数学模型的任务了，但是我们的目标是得到最为合适的权重参数θ

问题3：该如何求解θ呢：

　　参数问题结合概率，立即将思维转化到极大似然估计的频道上

　　似然函数：

　　对数似然：

　　对于似然函数，我们要求的是最大值，令，求解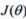的最小值即可

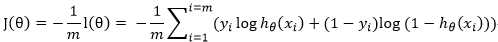
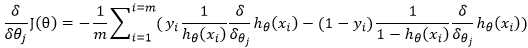
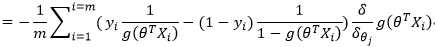
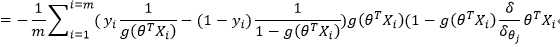
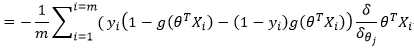
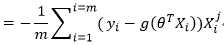
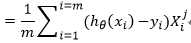
　　参数更新：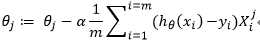

　　j:表示的是一个样本中的第j个特征,例如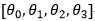：，j就表示θ的下标

　　i:表示第i个样本

2.逻辑回归关于二分类问题的理解

标签：span   回归   一个   似然函数   strong   两种   构建   nbsp   表示   

原文地址：https://www.cnblogs.com/houzichiguodong/p/9139561.html