标签:top padding 父节点 info The #define 组成 第三部分 src
disjoint-set data structure
union-find data structure
merge-find set

记号
#define fori(n) for(int i=0;i<(n);i++)
#define Mem(x) memset((x),0,sizeof(x));
定义
树形的数据结构,用于处理不相交集合的合并与查询问题;
但不支持分割集合
应用
判断两个点是否在同一联通块内,增加一条边是否产生环
实现
用数组储存,[树]结构实现
用数字代表元素:
parent(x)表示x在树形结构上的父节点对应的数字,
用代表元表示每个联通块.
举例说明
现在有编号为 2,4,6的三个结点
如果 p[2]=4;表明 2号结点指向 4号结点
4号结点表示 {2,4} 联通块
操作
结构
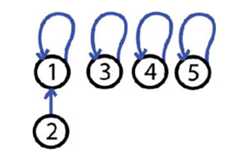
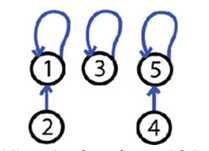
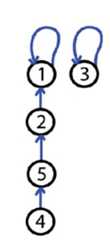
使用两个优化要点达到近乎常数时间
让更"矮"的树的根指向更"高"的树
建立数组rank[]来判断树深度,
CREATE-SET(x)时,rank[x]=0,
当MERGE时,rank更大的根将成为更小的根的parent;如果两根rank相同,就任选一个父根,并且增加父根的root的值
|
void unite(int x,int y){ int yy=find(y); //if(xx==yy) return; if(rank[xx]<rank[yy]) p[xx]=yy; else p[yy]=xx;
if(rank[xx]==rank[yy]) rank[xx]++; |
make each node on the find path point directly to the root
具体见find函数的代码部分
加深印象
https://www.hackerearth.com/zh/practice/notes/disjoint-set-union-union-find/
可以访问诸如↑网站,可以看到丰富的图像,用图片来解释unionset
代码
最基本的由三部分组成
void init(int n);
int find(int);
void unite(int a,int b);
前两部分基本上都一样
第三部分还可以优化,优化的方式也不同
init()
就那样
|
void init(int n){fori(n)p[i]=i;}//注意题目中的编号是否从1开始 |
|
void init(int n){ //union by rank p[i]=i; } |
find()
|
int find(int x){return p[u]==u?u:p[u]=find(p[u]);} |
|
void unite(int a,int b){ p[find(b)]=find(a); } //b→{a所在联通块} |
|
void unite(int x,int y){ y=find(y); //if(x==y) return; if(rank[x]<rank[y]) p[x]=y; else p[y]=x;
if(rank[x]==rank[y]) rank[x]++; |
+各种应用需要的代码
|
/* 下标从 1 开始 */ int p[maxn]; set <int> point; //已经储存了并查集中的所有点 int flag; //是否有环 int cnt; //不同集合的合并次数 int size[maxn]; // 表示联通块含有的元素数量 int init(int n) { point.clear(); fori(n) { p[i] = i; size[i] = 1; } cnt=0; flag=0; } int find(int u) { return p[u]==u?u:p[u]=find(p[u]); } void unite(int a,int b) { int aa=find(a); int bb=find(b); if(aa==bb){ flag=1; }else if(size(aa)<size(bb)){ cnt++; p[aa]=bb; size[bb]+=size[aa]; }else{ cnt++; p[bb]=aa; size[aa]+=size[bb]; } } |
时间复杂度研究
假设创建了n次集合,使用了f次find操作
不用任何优化
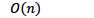
仅使用路径压缩
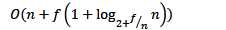
仅使用union by rank/size
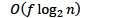
两次优化
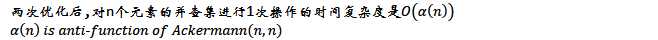
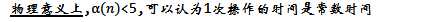
标签:top padding 父节点 info The #define 组成 第三部分 src
原文地址:https://www.cnblogs.com/migeater/p/9141539.html