标签：应用 直接 灵活 随机梯度 适合 抽取 出现 style 慢慢
一、随机梯度下降法基础
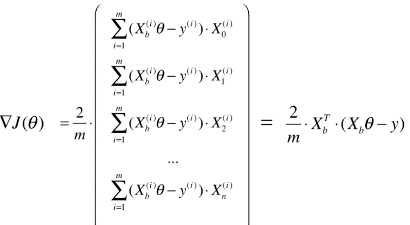
# 梯度中的每一项计算：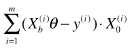
，要计算所有样本（共 m 个）；
# 批量梯度下降法的思路：计算损失函数的梯度，找到优化损失函数的最近距离，或者称最直接的方向；
# 批量梯度下降法的梯度计算：每一次都对数据集中的所有样本的所有数据进行计算；
# 特点：
# 计算每一个 theta 值对应的梯度时，计算量较大；
# 是损失函数减小最快的方向
# 随机梯度下降法思路：在计算梯度中的一项时，不是计算所有样本的数据，而是只随机抽取一个样本进行计算；
# 公式变形：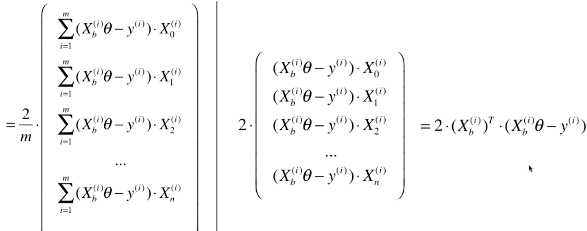
# 新的搜索方向计算公式（也即是优化的方向）：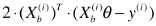
# 根据此搜索方向，逐步寻找损失函数的最小值
# 此处称为搜索方向，而不是梯度的计算公式，因为此公式已经不是梯度公式，而表示优化损失函数的方向；
# 目标：寻找最佳模型对应的参数
# 最佳模型：损失函数的最小值时所对应的模型；
# 得到最佳模型的方案：优化损失函数，找到其最小值；
# 优化损失函数的方案：寻找能使损失函数减小的方向，按此方向逐步优化损失函数，得到其最小值；
# 损失函数的梯度是损失函数减小最快的方向，也就是每一个 theta 的变化量，对应的损失函数的变化量最大；
# 为什么要找损失函数的最小值：
# 损失函数是线性模型的一部分
# 线性模型为拟合住数据的数学模型
# 损失函数的取值越小，表示模型拟合住的数据量越多，则该模型对数据的预测越精确；
# 随机梯度下降法的搜索路径：
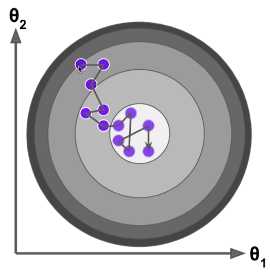
# 特点：
# 每一次搜索的方向，不能保证是损失函数减小的方向；
# 每一次搜索的方向，不能保证是损失函数减小最快的方向；
# 其优化方向具有不可预知性；
# 意义：
# 实验结论表明，即使随机梯度下降法的优化方向具有不可预知性，通过此方法依然可以差不多来到损失函数最小值的附近，虽然不像批量梯度下降法那样，一定可以来到损失函数最小值位置，但是，如果样本数量很大时，有时可以用一定的模型精度，换取优化模型所用的时间；
# 实现技巧：确定学习率（η：eta）的取值，很重要；
# 原因：在随机梯度下降法优化损失函数的过程中，如果 η 一直取固定值，可能会出现，已经优化到损失函数最小值位置了，但由于随机的过程不够好，η 又是各固定值，导致优化时慢慢的又跳出最小值位置；
# 方案：优化过程中让 η 逐渐递减（随着梯度下降法循环次数的增加，η 值越来越小）；
# η 的去顶过程：
# 1）如果：η = 1 / i_iters；（i_iters：当前循环次数）
# 问题：随着循环次数（i_iters）的增加，η 的变化率差别太大；
# 2）如果：η = 1 / (i_iters + b)；（b：为常量）
# 解决了 η 的变化率差异过大
# 3）再次变形：η = a / (i_iters + b)；（a、b：为常量）
# 分子改为 a ，增加 η 取值的灵活度；
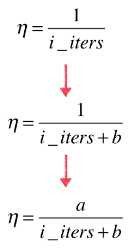
# a、b：为随机梯度下降法的超参数；
# 本次学习不对 a、b 调参，选用经验上比较适合的值：a = 5、b = 50；
# 随机梯度下降法特点：
# 学习率随着循环次数的增加，逐渐递减；
# 这种逐渐递减的思想，是模拟在搜索领域的重要思路：模拟退火思想；
# 模拟退火思想：在退火过程中的冷却函数，温度与冷却时间的关系；
# 一般根据模拟退火思想，学习率还可以表示：η = t0 / (i_iters + t1)
二、实现随机梯度下降法
标签：应用 直接 灵活 随机梯度 适合 抽取 出现 style 慢慢
原文地址：https://www.cnblogs.com/volcao/p/9144362.html
