标签:fun app pre 时间复杂度 ati ace orm for linear
ridge regression: 在最小二乘的基础上添加一个系数为α的惩罚项,惩罚项为参数向量2范数的平方,可以通过控制α来调节数据集的过拟合问题
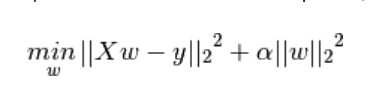
拟合方法,参数调用与线性回归相同
岭回归优点:可以应用于高度坏条件矩阵(目标值的轻微改变会造成参数的大方差,数据曲线波动加剧,容易导致过拟合问题,因此添加系数为α的惩罚项减小波动)
当α很大时,为了使模型达到最小值,惩罚项必须趋于零,此时主要考虑平方损失;当α趋近于0时,参数向量方差很大,容易导致过拟合。
对于岭回归,重点为调整α使平方损失与参数损失达到平衡。
import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model # X is the 10x10 Hilbert matrix 生成10×10的希尔伯特矩阵和全1矩阵 X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis]) y = np.ones(10) # ############################################################################# # Compute paths n_alphas = 200 #将α从10的-10到10的-2分为200个数 alphas = np.logspace(-10, -2, n_alphas) coefs = [] for a in alphas: ridge = linear_model.Ridge(alpha=a, fit_intercept=False)#生成ridge对象,不考虑截距 ridge.fit(X, y)#采用对象的fit方法进行岭回归拟合 coefs.append(ridge.coef_) # ############################################################################# # Display results ax = plt.gca() #生成一个plot对象 ax.plot(alphas, coefs) #绘图 ax.set_xscale(‘log‘)#以log为单位绘制坐标间隔 ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis坐标值以-1分隔, plt.xlabel(‘alpha‘) plt.ylabel(‘weights‘) plt.title(‘Ridge coefficients as a function of the regularization‘) plt.axis(‘tight‘)#不改变x,y的范围尽量将数据移动至图片的中央 plt.show()
1. 岭回归的时间复杂度为O(np2)
2. RidgeCV:在不同的α值时,通过交叉验证得出最优α
RidgeCV(alphas=[0.1, 1.0, 10.0], cv=None, fit_intercept=True, scoring=None, normalize=False)
CV默认为留1验证
sklearn help之岭回归 ridge regression
标签:fun app pre 时间复杂度 ati ace orm for linear
原文地址:https://www.cnblogs.com/yxr-blogs/p/9144131.html