标签:set condition size tac open letters nbsp 中间 tput
You are given a string s consisting of n lowercase Latin letters.
Let‘s denote k-substring of s as a string subsk?=?sksk?+?1..sn?+?1?-?k. Obviously, subs1?=?s, and there are exactly 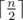 such substrings.
such substrings.
Let‘s call some string t an odd proper suprefix of a string T iff the following conditions are met:
For evey k-substring (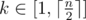 ) of s you have to calculate the maximum length of its odd proper suprefix.
) of s you have to calculate the maximum length of its odd proper suprefix.
The first line contains one integer n (2?≤?n?≤?106) — the length s.
The second line contains the string s consisting of n lowercase Latin letters.
Print 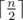 integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or ?-?1, if there is no such string that is an odd proper suprefix of i-substring).
integers. i-th of them should be equal to maximum length of an odd proper suprefix of i-substring of s (or ?-?1, if there is no such string that is an odd proper suprefix of i-substring).
15
bcabcabcabcabca
9 7 5 3 1 -1 -1 -1
24
abaaabaaaabaaabaaaabaaab
15 13 11 9 7 5 3 1 1 -1 -1 1
19
cabcabbcabcabbcabca
5 3 1 -1 -1 1 1 -1 -1 -1
The answer for first sample test is folowing:
思路一:考虑用hash值判断字符串等价性。对于每个查询点,我们正常二分长度是不满足单调性的;于是我们转换思路,不对单点二分,而是对于每个固定的答案中心点,因为其对称的另外的点是固定的,因此可以二分求出最大匹配长度,如对于mi,最大匹配长度是2 * x + 1,则更新ans[mi - x] = max(ans[mi - x], 2 * x + 1)。这样枚举完中间点之后,我们并没有做完,因为我们只更新了每个中心点最大匹配长度对应的起点的答案,但相同的中心点,也可能作为其他起点取到最大值的中心点,因此对于每个ans[i],先将其赋为max(ans[i], ans[i - 1] - 2)。这样扫一遍ans数组就行了。瓶颈在于预处理,nlogn。

1 #include <iostream> 2 #include <fstream> 3 #include <sstream> 4 #include <cstdlib> 5 #include <cstdio> 6 #include <cmath> 7 #include <string> 8 #include <cstring> 9 #include <algorithm> 10 #include <queue> 11 #include <stack> 12 #include <vector> 13 #include <set> 14 #include <map> 15 #include <list> 16 #include <iomanip> 17 #include <cctype> 18 #include <cassert> 19 #include <bitset> 20 #include <ctime> 21 22 using namespace std; 23 24 #define pau system("pause") 25 #define ll long long 26 #define pii pair<int, int> 27 #define pb push_back 28 #define mp make_pair 29 #define clr(a, x) memset(a, x, sizeof(a)) 30 31 const double pi = acos(-1.0); 32 const int INF = 0x3f3f3f3f; 33 const int MOD = 1e9 + 7; 34 const double EPS = 1e-9; 35 const int B = 131; 36 37 int n; 38 char s[1000015]; 39 ll Hash[1000015], pp[1000015]; 40 ll get_Hash(int s, int e) { 41 ll res = (Hash[e] - pp[e - s + 1] * Hash[s - 1]) % MOD; 42 if (res < 0) res += MOD; 43 return res; 44 } 45 int ans[1000015]; 46 bool check(int mi, int x) { 47 return get_Hash(mi - x + 1, mi + x - 1) == get_Hash(n + 1 - mi - x + 1, n + 1 - mi + x - 1); 48 } 49 int main() { 50 scanf("%d %s", &n, s + 1); 51 pp[0] = 1; 52 for (int i = 1; i <= n; ++i) { 53 Hash[i] = (Hash[i - 1] * B + s[i]) % MOD; 54 pp[i] = pp[i - 1] * B % MOD; 55 } 56 clr(ans, -1); 57 for (int i = 1; i <= n + 1 >> 1; ++i) { 58 int s = 1, e = i, mi, res = 0; 59 if (2 * i == n + 1) break; 60 while (s <= e) { 61 mi = s + e >> 1; 62 if (check(i, mi)) s = (res = mi) + 1; 63 else e = mi - 1; 64 } 65 ans[i - res + 1] = max(ans[i - res + 1], 2 * res - 1); 66 } 67 for (int i = 1; i <= n + 1 >> 1; ++i) { 68 ans[i] = max(ans[i - 1] - 2, ans[i]); 69 printf("%d ", ans[i]); 70 } 71 return 0; 72 }
思路二:我们注意到性质ans[i] >= ans[i - 1] + 2, 也就是ans[i - 1] <= ans[i] - 2.因此我们从后往前扫ans数组,每个点从ans[i] - 2暴力向下枚举,找到答案就是最终解,并马上break。这样总体的步幅顶多n + 2 * n。复杂度O(n)。

1 #include <iostream> 2 #include <fstream> 3 #include <sstream> 4 #include <cstdlib> 5 #include <cstdio> 6 #include <cmath> 7 #include <string> 8 #include <cstring> 9 #include <algorithm> 10 #include <queue> 11 #include <stack> 12 #include <vector> 13 #include <set> 14 #include <map> 15 #include <list> 16 #include <iomanip> 17 #include <cctype> 18 #include <cassert> 19 #include <bitset> 20 #include <ctime> 21 22 using namespace std; 23 24 #define pau system("pause") 25 #define ll long long 26 #define pii pair<int, int> 27 #define pb push_back 28 #define mp make_pair 29 #define clr(a, x) memset(a, x, sizeof(a)) 30 31 const double pi = acos(-1.0); 32 const int INF = 0x3f3f3f3f; 33 const int MOD = 1e9 + 7; 34 const double EPS = 1e-9; 35 const int B = 131; 36 37 int n; 38 char s[1000015]; 39 ll Hash[1000015], pp[1000015]; 40 ll get_Hash(int s, int e) { 41 ll res = (Hash[e] - pp[e - s + 1] * Hash[s - 1]) % MOD; 42 if (res < 0) res += MOD; 43 return res; 44 } 45 int ans[1000015]; 46 bool check(int mi, int x) { 47 return get_Hash(mi - x + 1, mi + x - 1) == get_Hash(n + 1 - mi - x + 1, n + 1 - mi + x - 1); 48 } 49 int main() { 50 scanf("%d %s", &n, s + 1); 51 pp[0] = 1; 52 for (int i = 1; i <= n; ++i) { 53 Hash[i] = (Hash[i - 1] * B + s[i]) % MOD; 54 pp[i] = pp[i - 1] * B % MOD; 55 } 56 clr(ans, -1); 57 for (int i = n + 1 >> 1; i; --i) { 58 int l = i, r = n + 1 - i; 59 if (l == r) { 60 ans[i] = -1; 61 continue; 62 } 63 for (int j = ans[i + 1] + 2; ~j; j -= 2) { 64 if (get_Hash(l, l + j - 1) == get_Hash(r - j + 1, r)) { 65 ans[i] = j; 66 break; 67 } 68 } 69 } 70 for (int i = 1; i <= n + 1 >> 1; ++i) { 71 printf("%d ", ans[i]); 72 } 73 return 0; 74 }
Educational Codeforces Round 41 (Rated for Div. 2) F. k-substrings
标签:set condition size tac open letters nbsp 中间 tput
原文地址:https://www.cnblogs.com/BIGTOM/p/9146337.html