标签:bubuko row 位置 角度 不完全 2-2 图像 参数 划算
还是用例子说比较好些。
(2018宝鸡市二检理科第10题)关于\(x\)的方程\(\sqrt{3}sin2x+cos2x-k-1=0\)在\([0,\cfrac{\pi}{2}]\)内有两个实数根,则\(k\)的取值范围是()。
A.\((1,2)\) \(\hspace{2cm}\) B.\([0,2)\) \(\hspace{2cm}\) C.\([0,1)\) \(\hspace{2cm}\) D.\([-2,1)\)
遇到这样的题目,我们一般是这样做的,先转化为\(k+1=2sin(2x+\cfrac{\pi}{6}),x\in [0,\cfrac{\pi}{2}]\),
然后分别作出函数\(y=k+1\)和函数\(y=2sin(2x+\cfrac{\pi}{6}),x\in [0,\cfrac{\pi}{2}]\)的图像,
利用图像就可以知道,要使得两个函数有两个交点,需要满足\(1\leq k+1<2\),解得\(0\leq k<1\),故选C。
上述变形中,当将原方程转化为\(k+1=2sin(2x+\cfrac{\pi}{6})\),就已经将参数和自变量分离开了,这样的方法自然就叫分离参数法。
还是用上例说事,像这样的方程由于含有\(sin2x\)等,我们就称为超越方程,意思是不能像解\(x^2+3x+2=0\)这样的代数方程一样把她解出来。从数的角度行不通,那就只能考虑从形的角度了,如果我们设函数为\(y=\sqrt{3}sin2x+cos2x-k-1\),那么这个函数就不太好作图,但是如果分离成\(k+1=2sin(2x+\cfrac{\pi}{6})\),则原方程的实数根的个数问题,就自然转化为两个函数\(y=k+1\)和\(y=2sin(2x+\cfrac{\pi}{6})\)的图像的交点的个数问题了,而且这两个函数的图像都很好作图,一下子就把问题的难度降下来了。通过这个例子,我们初步体会了分离常数法的优越性。
再看个题目的解答,然后我们回答这个问题。
 \(\fbox{例1}\)(2017西安模拟)
\(\fbox{例1}\)(2017西安模拟)
已知函数\(f(x)=kx^2-lnx\)有两个零点,求参数\(k\)的取值范围。
A、\(k>\cfrac{e}{2}\) \(\hspace{2cm}\) B、\(0<k<\sqrt{e}\) \(\hspace{2cm}\) C、\(k>\cfrac{\sqrt{2}e}{2}\) \(\hspace{2cm}\) D、 \(0<k<\cfrac{1}{2e}\)
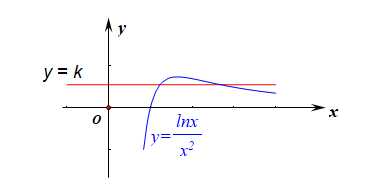
分析:函数的定义域为\((0,+\infty)\),由函数\(f(x)=kx^2-lnx\)有两个零点,转化为方程\(kx^2=lnx\)有两个不同的实数根,
再转化为\(k=\cfrac{lnx}{x^2}\)有两个不同的实数根,再转化为函数\(y=k\)和函数\(y=g(x)=\cfrac{lnx}{x^2}\)的图像有两个不同的交点,
用导数研究函数\(g(x)\)的单调性,\(g'(x)=\cfrac{\cfrac{1}{x}\cdot x^2-lnx\cdot 2x}{(x^2)^2}=\cfrac{1-2lnx}{x^3}\),
令\(1-2lnx>0\),得到\(0<x<\sqrt{e}\),令\(1-2lnx<0\),得到\(x>\sqrt{e}\),
即函数\(g(x)\)在区间\((0,\sqrt{e}]\)上单调递增,在\([\sqrt{e},+\infty)\)上单调递减,
故\(g(x)_{max}=g(\sqrt{e})=\cfrac{1}{2e}\),
作出函数\(g(x)\)和函数\(y=k\)的简图,由图像可得\(k\)的取值范围是\(k\in(0,\cfrac{1}{2e})\)。
从上述的解法中(当然本题还有其他的解法,比如转化为方程\(kx^2=lnx\)有两个不同的实数根,带参讨论法),我们体会到,如果一个数学题目从数的角度直接来求解,
结果很有可能要么不会求解,要么解不出,更或者没有思路;此时若换个角度思考,从形入手分析,将参数或含有参数的代数式(比如\(k+1\))和自变量分别放置在等号的两端,
即\(k=f(x)\)的形式,然后数的问题就转化为形的问题了,从而直观快捷,思路简单明了。一句话,从形的角度解题的前提就是施行分离参数的方法。
①常规法分类参数:如\(\lambda f(x)=g(x)\Rightarrow \lambda=\cfrac{g(x)}{f(x)}\);
②倒数法分离参数:如\(\lambda f(x)=g(x)\Rightarrow \lambda=\cfrac{g(x)}{f(x)}\);
③讨论法分离参数:如\(\lambda f(x)\ge g(x)\);
④整体法分离参数:如\(\lambda^2+2\lambda=f(x)\);
⑤不完全分离参数法:如\(\cfrac{b}{x}=lnx+x-x^2\);
⑥作商法凸显参数,换元法凸显参数;
但是,不是所有的含参问题都适合分离参数,比如\(ax^2-a^2x+3<0\)在区间\([1,2]\)上恒成立,求\(a\)的范围,
那就不能用分离参数的方法,因为你没法将参数和自变量有效的分开,所以此时你可能需要借助二次函数的图像来考虑,而不是一味的使用分离参数法。
一般来说,以下的一些情形都不适合使用分离参数法:
比如,已知方程\(e^{-x}=ln(x+a)\)在\(x>0\)时有解,求参数的取值范围;
本题目就不能将参数和自变量有效的分离开的,
此时我们就可以考虑用数形结合的思路求解。解法
引例,已知函数\(f(x)=x^2+ax-2a\ge 0\)对\(x\in [1,5]\)上恒成立,求参数\(a\)的取值范围。
如果用分离参数的方法,则先转化为\((x-2)a\ge -x^2,x\in [1,5]\)
接下来就转化成了三个恒成立的命题了,不管会不会做,从效率上都已经很不划算了。
【法1】分类讨论如下:
当\(x=2\)时,原不等式即\((2-2)a\ge -4\),\(a\in R\)都符合题意;
当\(2<x<5\)时,原不等式等价于\(a\ge \cfrac{-x^2}{x-2}=-(x-2)-\cfrac{4}{x-2}-4=g(x)\)恒成立;
\(g(x)=-(x-2)-\cfrac{4}{x-2}-4\leq 2\sqrt{(x-2)\cdot \cfrac{4}{x-2}}-4=-8\)
求得当\(x=4\)时,\(g(x)_{max}=-8\),故\(a\ge -8\)
当\(1<x<2\)时,原不等式等价于\(a\leq \cfrac{-x^2}{x-2}=-(x-2)-\cfrac{4}{x-2}-4=g(x)\)恒成立;
\(g(x)=-(x-2)-\cfrac{4}{x-2}-4\ge 2\sqrt{-(x-2)\cdot \cfrac{-4}{x-2}}-4=0\)
当且仅当\(x=0\)时取到等号,并不满足前提条件\(1<x<2\),故是错解。
此时需要借助对勾函数的单调性,函数\(y=x+\cfrac{4}{x}\)在区间\([1,2]\)上单调递增,
那么\(y=x-2+\cfrac{4}{x-2}\)在区间\([1,2]\)上单调递减,
\(y=-(x-2)-\cfrac{4}{x-2}\)在区间\([1,2]\)上单调递增,\(y=-(x-2)-\cfrac{4}{x-2}-4\)在区间\([1,2]\)上单调递增,
故\(g(x)_{min}=g(1)=1\),故\(a\leq 1\)
以上三种情况取交集(由于是针对自变量分类讨论的,要求不管什么情况下都必须恒成立,故最后必须求交集),得到\(a\in [-8,1]\)。
很明显,这时候就将一个题目做成了三个题目,从效率上很不划算。
那么,该怎么做呢? 注意到函数\(f(x)=x^2+ax-2a\)是二次函数,故可以利用二次函数来求解。
【法2】①由于\(\Delta=a^2+8a≤0\)时满足题意,解得\(-8≤a≤0\);
再考虑对称轴\(x=-\cfrac{a}{2}\)和给定区间\([1,5]\)的相对位置关系
②当\(-\cfrac{a}{2}≤1\)时,即\(a≥-2\)时,函数\(f(x)\)在区间\([1,5]\)单调递增,
所以\(f(x)_{min}=f(1)=1+a-2a≥0\),解得\(-2≤a≤1\),又因为\(a≥-2\),所以得到\(-2≤a≤1\);
③当\(-\cfrac{a}{2}≥5\)时,即\(a≤-10\)时,函数\(f(x)\)在区间\([1,5]\)单调递减,
所以\(f(x)_{min}=f(5)=25+5a-2a≥0\),解得\(a≥-\cfrac{25}{3}\),又因为\(a≤-10\),所以得到\(a\in\varnothing\);
④当\(1<-\cfrac{a}{2}<5\),即\(-10<a<-2\)时,\(f(x)_{min}=f(-\cfrac{a}{2})=\cfrac{a^2}{4}-\cfrac{a^2}{2}-2a≥0\),
得到\(-8≤a≤0\),又\(-10<a<-2\),所以\(-8≤a<-2\)(这种情形可以省略)
综上可得\(a\)的取值范围是\([-8,1]\)
【法3】其实,如果参数的系数能取到正、负、零三种情形的,直接分离麻烦,此时我们还可以尝试倒数法分离参数,
由题目可以变形为\(\cfrac{a(x-2)}{x^2}\ge -1\),\(x\in [1,5]\),此时我们考虑将参数\(a\)放到不等式的右边去,故分类讨论如下:
①当\(a=0\)时,原不等式\(0\ge -1\)恒成立,故满足题意;
当\(a>0\)时,不等式变形为\(-\cfrac{1}{a}\leq \cfrac{x-2}{x^2}\)恒成立;当\(a<0\)时,不等式变形为\(-\cfrac{1}{a}\ge \cfrac{x-2}{x^2}\)恒成立;
我们一并研究上述两个不等式右端的函数性质,
令函数\(h(x)=\cfrac{x-2}{x^2}\),\(x\in [1,5]\),则\(h'(x)=\cfrac{x^2-(x-2)\cdot 2x}{x^4}=\cfrac{-x^2+4x}{x^4}= \cfrac{4-x}{x^3}\);
故函数\(h(x)\)在区间\([1,4]\)上单调递增,在区间\([4,5]\)上单调递减,
故\(h(x)_{max}=h(4)=\cfrac{1}{8}\),\(h(x)_{min}=min\{h(1),h(5)\}=h(1)=-1\);承上可知,
②当\(a>0\)时,不等式变形为\(-\cfrac{1}{a}\leq \cfrac{x-2}{x^2}\)恒成立,
即\(-\cfrac{1}{a}\leq h(x)_{min}=-1\),从而解得\(0<a\leq 1\);
③当\(a<0\)时,不等式变形为\(-\cfrac{1}{a}\ge \cfrac{x-2}{x^2}\)恒成立,
即\(-\cfrac{1}{a}\ge h(x)_{max}=\cfrac{1}{8}\),从而解得\(-8\leq a<0\);
综上所述,以上三种情况取并集(由于这种解法思路是针对参数分类讨论的,故最后必须求并集),得到\(a\in [-8,1]\)。
比如函数\(f(x)=x^2-2x+a(e^{x-1}+e^{-x+1})\)有唯一的零点,
分离参数后,得到\(a=\cfrac{-x^2+2x}{e^{x-1}+e^{-x+1}}=h(x)\),
你确信你能用研究清楚函数\(h(x)\)的性质,并用手工做出函数的图像吗?省省吧,您呐。
比如已知\(2a-1+sin2x+a(sinx-cosx)\ge 0\)在\(x\in [0,\cfrac{\pi}{2}]\)上恒成立,求参数\(a\)的取值范围。\([1,+\infty)\)
接下来的思路有:
思路一:分离参数,当分离为\(a\ge \cfrac{1-sin2x}{2+sinx-cosx}=g(x)\)时,你会发现,求函数\(g(x)_{max}\)很难,所以放弃;
思路二:链接,转化划归,令\(sinx-cosx=t=\sqrt{2}sin(x-\cfrac{\pi}{4})\),由于\(x\in [0,\cfrac{\pi}{2}]\),故\(t\in [-1,1]\)
由\((sinx-cosx)^2=t^2\),得到\(sin2x=1-t^2\),故不等式转化为\(at+1-t^2+2a-1\ge 0\),
即\(t^2-at-2a\leq 0\)在\(t\in [-1,1]\)上恒成立,令\(h(t)=t^2-at-2a,t\in [-1,1]\),
则\(h(t)\leq 0\)等价于\(\begin{cases}h(-1)=1+a-2a\leq 0\\h(1)=1-a-2a\leq 0 \end{cases}\)
解得\(a\ge 1\),
解后反思:
1、已知含参函数\(f(x)\)的单调性(比如单增),求参数的取值范围,等价于\(f'(x)\ge 0\),且还需要验证等号时不能让函数\(f(x)\)称为常函数,不过解答题一般不需要验证,是因为给定的函数比较复杂,当参数取到某个值是一般不会称为常函数。
2、转化为已知恒成立问题,求参数范围,一般首选分离参数的思路。
3、关于三角函数的这种转化必须熟练掌握。三角函数的转化
4、二次函数在某个区间上恒成立问题的模型必须熟练掌握。二次函数恒成立模型
已知函数\(f(x)=x^2-ax\),\(g(x)=mx+nlnx\),函数\(f(x)\)的图像在点\((1,f(1))\)处的切线的斜率为\(1\),函数\(g(x)\)在\(x=2\)处取到极小值\(2-2ln2\);
(1)求函数\(f(x)\)与\(g(x)\)的解析式;
分析:由题可知\(f'(x)=2x-a\),又\(f'(1)=2-a=1\),解得\(a=1\),即\(f(x)=x^2-x\);
又\(g'(x)=m+\cfrac{n}{x}\),由\(g'(2)=m+\cfrac{n}{2}=0\)及\(g(2)=2m+nln2=2-2ln2\),解得\(m=1,n=-2\),即\(g(x)=x-2lnx\);
(2)已知函数\(f(x)+g(x)\ge x^2-\lambda(x-1)\)对任意的\(x\in(0,1]\)恒成立,求实数\(\lambda\)的取值范围。
分析:由于\(f(x)+g(x)=x^2-2lnx\),则\(x^2-2lnx\ge x^2-\lambda(x-1)\)对任意的\(x\in(0,1]\)恒成立,可以有以下的思路:
法1:带参分析法,先令\(h(x)=\lambda(x-1)-2lnx\),则问题转化为\(h(x)\ge 0\)对任意的\(x\in(0,1]\)恒成立,
\(h'(x)=\lambda-\cfrac{2}{x}=\cfrac{\lambda x-2}{x}\)
当\(\lambda\leq 0\)时,\(h'(x)<0\),\(h(x)\)在区间\((0,1]\)上单调递减,
\(h(x)_{min}=h(1)=0\),即\(h(x)\ge 0\)恒成立;
当\(0<\lambda \leq 2\)时,\(h'(x)<0\),\(h(x)\)在区间\((0,1]\)上单调递减,
\(h(x)_{min}=h(1)=0\),即\(h(x)\ge 0\)恒成立;
当\(\lambda>2\)时,\(h'(x)<0\)在\((0,\cfrac{2}{\lambda})\)上恒成立,\(h'(x)>0\)在\((\cfrac{2}{\lambda},1)\)上恒成立,
即\(h(x)\)在\((0,\cfrac{2}{\lambda})\)单调递减,在\((\cfrac{2}{\lambda},1)\)上单调递增,
所以\(h(\cfrac{2}{\lambda})<h(1)=0\),故不满足题意,注意\(h(1)=0\),即函数\(h(x)\)恒过点\((1,0)\)
综上所述,实数\(\lambda\)的取值范围为\((-\infty,2]\)。
法2:讨论法分离参数,先转化为\(\lambda(x-1)\ge 2lnx\)对任意的\(x\in(0,1]\)恒成立,
当\(x=1\)时,\(\lambda\cdot 0\ge 2ln1=0\),\(\lambda\in R\);
当\(x\in (0,1)\)时,分离参数得到\(\lambda \leq \cfrac{2lnx}{x-1}\);令\(h(x)= \cfrac{2lnx}{x-1}\),
\(h'(x)=\cfrac{\cfrac{2}{x}(x-1)-2lnx}{(x-1)^2}=\cfrac{2(1-\cfrac{1}{x}-lnx)}{(x-1)^2}\);
令\(m(x)=1-\cfrac{1}{x}-lnx\),则\(m'(x)=\cfrac{1}{x^2}-\cfrac{1}{x}=\cfrac{1-x}{x^2}\),
则\(m'(x)>0\),则\(m(x)\)在\((0,1)\)上单调递增,故\(m(x)<m(1)=0\),故\(h'(x)=\cfrac{2m(x)}{(x-1)^2}<0\),
则\(h(x)\)在\((0,1)\)上单调递减,故\(h(x)>h(1)=2\)(由洛必达法则求得),即\(\lambda\leq 2\)
综上所述求交集得到,\(\lambda \in(-\infty,2]\)。
法3:不完全分离参数法,由\(\lambda(x-1)\ge 2lnx\)对任意的\(x\in(0,1]\)恒成立,
做函数\(y=\lambda(x-1)\)和函数\(y=2lnx\)的图像,示意图
设直线\(y=\lambda(x-1)\)与曲线\(y=2lnx\)相切于点\((x_0,y_0)\),则有\(\cfrac{2}{x_0}=\lambda\),\(y_0=2lnx_0\),\(y_0=\lambda(x_0-1)\),
求得切点坐标\((1,0)\),此时\(\lambda=2\),由\(\lambda\)的几何意义可知,\(\lambda\)的取值范围是\((-\infty,2]\)。
分离常数法,一般常用于恒成立问题、能成立问题(有解),或无解问题,或已知函数零点个数命题中的参数取值范围问题。
分离参数时,尽可能的使函数形式简单,这样求导数判断单调性就简单些,而参数形式复杂些或者简单些都无所谓,
比如方程\((2-a)x-2(1+lnx)+a=0\)在\((0,\cfrac{1}{2})\)上无解,求参数的最小值。
转化一:\(a=\cfrac{2+2lnx-2x}{1-x}=h(x)\);
转化二:\(\cfrac{2-a}{2}=\cfrac{lnx}{x-1}=h(x)\),
我们看到第二种转化就比第一种转化划归要好的多。
如函数\(f(x)=\begin{cases}x^2+4x,x\leq 0\\xlnx,x>0\end{cases}\),\(g(x)=kx-1\),若方程\(f(x)-g(x)=0\)在\(x\in(-2,2)\)有三个实根,则实数\(k\)的取值范围是【】
A.\((1,ln2\sqrt{e})\;\;\;\;\;\) B.\((ln2\sqrt{e},\cfrac{3}{2})\;\;\;\;\;\) C.\((\cfrac{3}{2},2)\;\;\;\;\;\) D.\((1,ln2\sqrt{e})\cup(\cfrac{3}{2},2)\;\;\;\;\;\)
分析:显然\(x=0\)不是方程\(f(x)-g(x)=0\)的根,故可变形为\(k=\cfrac{f(x)+1}{x}\),
设\(\phi(x)=\cfrac{f(x)+1}{x}=\begin{cases}x+\cfrac{1}{x}+4,x<0\\\cfrac{1}{x}+lnx,x>0\end{cases}\),即\(k=\phi(x)\)在\(x\in(-2,2)\)有三个实根,
用导数方法研究函数\(\phi(x)\)的单调性,做出其图像;
由图像可得,要使得函数\(y=k\)与函数\(y=\phi(x)\)有三个交点,则\(k\in (1,ln2\sqrt{e})\cup(\cfrac{3}{2},2)\)
标签:bubuko row 位置 角度 不完全 2-2 图像 参数 划算
原文地址:https://www.cnblogs.com/wanghai0666/p/8617323.html