标签:logs 机器 isp note 研究 || bsp font 过程
矩阵论是对线性代数的延伸,很有必要深入研究。研究矩阵论可以加深对PCA,SVD,矩阵分解的理解,尤其是第一章入门的线性空间的理解,在知识图谱向量化,self_attention等论文中会涉及大量的矩阵论的知识。本文对此做一个总结,分为以下结构:
第一部分:矩阵的线性空间,矩阵的意义;
第二部分:矩阵的范数理解,self_attention以及transD论文核心技术解读;
第三部分:矩阵的分解以及PCA,SVD
1.线性空间,矩阵的意义
这部分内容是理解矩阵的基础也是最关键的部分。对于线性空间的基本概念不必多解释,都说矩阵的本质是线性变换,这里有必要总结一下。一般而言,矩阵乘以向量后结果仍然是向量,相当于对向量进行了变换。这个变换包括方向和幅度,方向指的是坐标轴,幅度一般值向量的特征值。举一个最直观的例子:
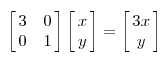 上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:
上面的M矩阵,其实已经是特征值了,呵呵。下面从最专业的矩阵论理论,具体解释矩阵的本质。前面的变换其实是对向量的左边进行拉伸或者旋转,所以先介绍一下在矩阵论中坐标轴,坐标系和坐标的概念。
对于线性空间Vn ,空间的基e1,e2,……是一组非线性相关向量,就是这些向量组成的行列式不为0。空间中的任一向量都可以写成这些基的线性组合,这些组合系数称之为向量的坐标。空间的基对应空间的坐标系,坐标是对应在坐标系中的。那么一个变换矩阵应该如何理解呢?现有空间里的一个向量x,Tx为向量的象,也就是经过变换后的向量。现推导如下:

首先半正定矩阵定义为: 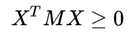
其中X 是向量,M 是变换矩阵
我们换一个思路看这个问题,矩阵变换中,MX代表对向量 X进行变换,我们假设变换后的向量为Y,记做Y = MX。于是半正定矩阵可以写成: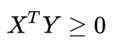
这个是不是很熟悉呢? 他是两个向量的内积。
同时我们也有公式:![]()
||X||,
||Y||代表向量 X,Y的长度,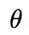 是他们之间的夹角。 于是半正定矩阵意味着
是他们之间的夹角。 于是半正定矩阵意味着![]()
, 这下明白了么?正定、半正定矩阵的直觉代表一个向量经过它的变化后的向量与其本身的夹角小于等于90度。
下面从上面推导的过程来理解,考虑矩阵的特征值:
若所有特征值均不小于零,则称为半正定。
若所有特征值均大于零,则称为正定。
矩阵经过特征值分解后的特征值是一个对角阵,就是原空间某一个基在变换后的空间的长度变化系数,大于0表示方向一致,小于0表示方向相反,每个向量都会经过变换矩阵A的每列系数组合变换,而A经过分解后分为特征值和坐标轴两部分,每个特征值表明了基的自身变换方向与幅度,>0表明同向变换。如果每个特征值都>0的话,由于向量是由空间的基线性组合而成最终导致变换后的向量与原向量同向变化。
2.矩阵的范数
矩阵的范数和向量的范数没有太大的不同,唯一添加的就是相容性。证明的矩阵的范数时只需证明4条就可以了。通常所说的矩阵一阶范数指的是列和范数,即取每列绝对值之和最大的数。矩阵的F范数应用是很广的。类似于用向量的欧式距离,把一个mxn的矩阵看成是碾平的向量,取欧氏距离即可。在self_attention论文中,核心就是矩阵的F范数结构化约束。有兴趣可以读一读并复现论文,用在工程之中。在知识图谱的transD论文里关于entity和relation的相互投影问题以及h和t不在一个空间的问题,可以很好地用矩阵论来解释。
3.矩阵的QR分解以及PCA,SVD
矩阵的QR分解理论对PCA和SVD具有非常好的指导意义。矩阵论里面非常好地阐释了QR分解和SVD的关系,这里不做推导了。PCA其实是SVD的外部封装。特征值分解和奇异值分解在机器学习领域都是属于满地可见的方法。两者有着很紧密的关系,特征值分解和奇异值分解的目的都是一样,就是提取出一个矩阵最重要的特征。先谈谈特征值分解吧:
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:![]() 这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:![]() 其中Q是这个矩阵A的标准正交特征向量系组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。这个结论其实是QR分解的一个推广,这个公式更能直观地解释第一部分关于半正定矩阵的解释。我们来看看奇异值分解和PCA的关系吧:
其中Q是这个矩阵A的标准正交特征向量系组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。这个结论其实是QR分解的一个推广,这个公式更能直观地解释第一部分关于半正定矩阵的解释。我们来看看奇异值分解和PCA的关系吧:








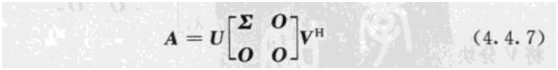





矩阵中关于奇异值的讲解,比网上其他的博客要正统很多。
标签:logs 机器 isp note 研究 || bsp font 过程
原文地址:https://www.cnblogs.com/txq157/p/9152515.html