POJ - 2184 Cow Exhibition

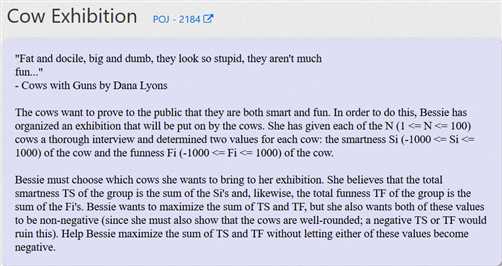
每只牛有智慧数值和滑稽值，你的目标是，从n之中挑选x只（可以是0）使得智慧之和和滑稽值和（两个都不能为
0）的总和最大

01背包（带负权）。很显然我们能选择智慧值做背包容量，来当01背包来做（也可以把滑稽值当背包容量），但
是我们要注意到不管是智慧值还是滑稽值都可能使负的，所以我们要分成两种情况。
1.s[i]>=0,就使普通的01背包，从后往前dp 
2.s[i]<0,从前往后进行dp。
第二种从前往后的原因：因为智慧值为负值，所以当前这个背包容量的价值是由j-s[i]（例：s[i]=-1,j=3,则
dp[3]=max(dp[3],dp[3-(-1)]+f[i])）转移过来的，所以使从前往后dp。

#define debug
#include<stdio.h>
#include<math.h>
#include<cmath>
#include<queue>
#include<stack>
#include<string>
#include<cstring>
#include<string.h>
#include<algorithm>
#include<iostream>
#include<vector>
#include<functional>
#include<iomanip>
#include<map>
#include<set>
#define pb push_back
#define dbg(x) cout<<#x<<" = "<<(x)<<endl;
#define lson l,m,rt<<1
#define cmm(x) cout<<"("<<(x)<<")";
#define rson m+1,r,rt<<1|1
using namespace std;
typedef long long ll;
const int maxn=1e5;
const int INF=0x3f3f3f3f;
const ll inf=0x7fffff;
const int mod=1e9+7;
const int MOD=10007;
//----
//define
int dp[maxn];
int s[maxn],f[maxn];
//solve
void solve() {
	int n,tots=0;
	cin>>n;
	for(int i=0; i<n; i++) {
		cin>>s[i]>>f[i];
		if(s[i]>=0)tots+=s[i];//偏移量（除负数外的最大背包容量）
	}
	memset(dp,-INF,sizeof(dp));
	dp[tots]=0;//因为背包容量不能为负值，所以加上偏移量，从tots开始（相当于原来01背包中的dp[0]=0） 
	for(int i=0; i<n; i++) {
		if(s[i]>=0)
			for(int j=2*tots; j>=s[i]; j--)dp[j]=max(dp[j],dp[j-s[i]]+f[i]);
		else for(int j=0; j<=2*tots+s[i]; j++)dp[j]=max(dp[j],dp[j-s[i]]+f[i]);
	}
	int ans=0;
	for(int i=tots; i<=2*tots; i++)
		if(dp[i]>0)ans=max(dp[i]+i-tots,ans);
	cout<<ans<<endl;
}

int main() {
	ios_base::sync_with_stdio(0);
#ifdef debug
	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
#endif
	cin.tie(0);
	cout.tie(0);
	solve();
	return 0;
}