标签：style img 图片 for src 了解 png family 数列
在正式介绍生成函数的计算之前我们要现引入泰勒公式，以便在之后我们使用。
泰勒公式：
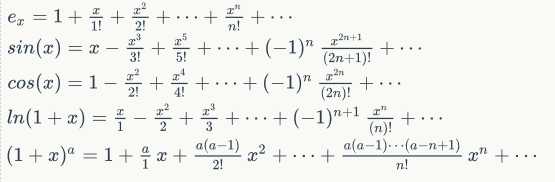
那在我们有了泰勒公式之后我们开始正式踏上我们的探索生成函数之旅...
PART 1 了解生成函数
对于一个数列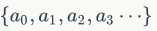
我们将他们整体表示成形如
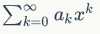的函数，然后将这个函数化简为封闭形式，最后所得的函数即为生成函数。
PART 2 求生成函数
斐波那契数列想必大家都知道，我们在这里就以他为例来讨论如何求生成函数，步骤如下：
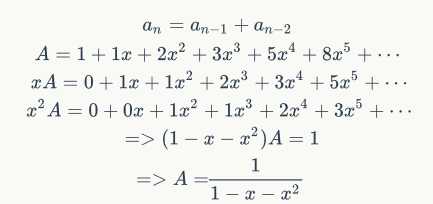
声明一下，带进去的x∈(0,1)。
可是总有些人得寸进尺，所以看到这里肯定有人要问：那斐波那契的通项公式是啥？
虽然通项公式和生成函数的关系不大，但我们在这里还是讲解一下如何根据斐波那契的生成函数求解它的通项公式：
$$ \begin{equation}
设1 - x - x^2 = (1 - k_1x)(1 - k_2x) \\
\therefore k_1 = \frac{\sqrt{5} - 1}{2} , k_2 = \frac{\sqrt{5} + 1}{2} \\
\therefore \frac{1}{1 - x - x^2} = \frac{a}{1 - k_1x} + \frac{b}{1 - k_2x} \\
=> a(1 - k_2x) + b(1 - k_1x) = 1 \\
\therefore
\end{equation} $$
标签：style img 图片 for src 了解 png family 数列
原文地址：https://www.cnblogs.com/yzxverygood/p/9180007.html
