双指针

标签：就是   tar   数量级   oop   需要   inter   course   双指针   ima   

有时候我们要对一个数组进行i和j两个下标的双重循环枚举：

　　如图，红色的i下标指向第一个元素时，绿色的j要从第二个元素到最后一个元素枚举一遍；i下标指向第2个元素时，绿色的j要从第3个元素到最后一个元素枚举一遍。以此类推。这是一个O(N2)的复杂度。

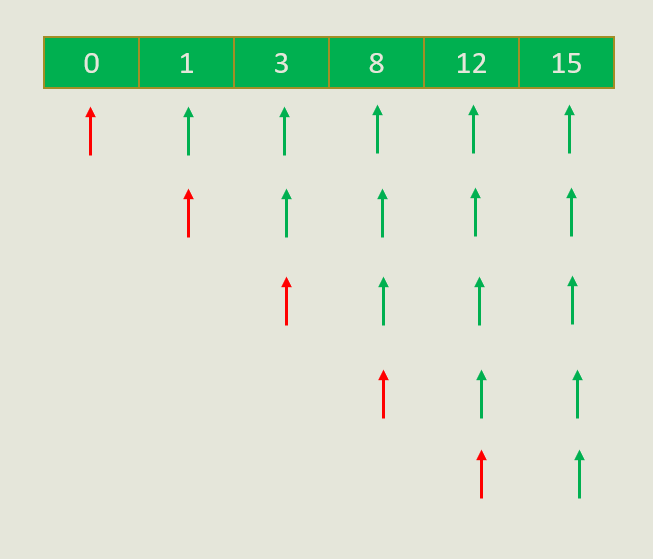
双指针的思路是什么呢？就是在某些情况下，根据题目要求，j下标并不需要从i+1开始重新向后枚举一遍，而是跟随着i向后移动，j也向后移动。

　　如图，当红色i下标向右移动时，绿色j下标是不会向左移动的。它有可能不动，也有可能向右，但是不会向左。由于j坐标不会向左移动，所以整个枚举的复杂度是O(N)的，比O(N2)低了一个数量级。

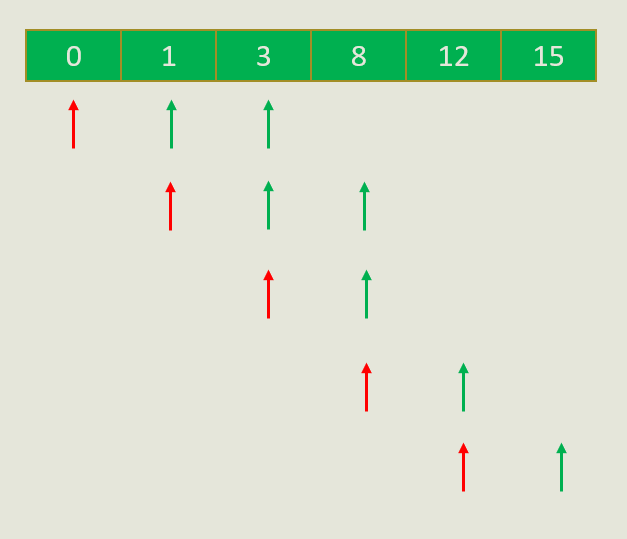
【例题分析】
　　给定N个整数A1， A2， … ，AN，以及一个正整数K。问在所有的大于等于K的两个数的差(Ai-Aj)中，最小的差是多少。(N <= 100000)

双指针优化：
首先就是对A数组排序。比如假设排好序的A数组是：
　　A=[1, 3, 7, 8, 10, 15], K=3
这时我们枚举两个数中较小的是A[i]，较大的数是A[j]；对于A[i]来说，我们要找到最优的A[j]，也就是最小的A[j]满足A[j]-A[i]>=k

如下图：

• 当A[i]=1的时候，最优的A[j]=7
• 当A[i]=3的时候，最优的A[j]=7
• 当A[i]=7的时候，最优的A[j]=10
• 当A[i]=8的时候，最优的A[j]=15
• 当A[i]=10的时候，最优的A[j]=15

　　当i依次向右的时候，这个“最优的A[j]”或者不动或者向右，不会向左。换句话说，我现在已知A[i]=1的时候A[j]=7是最优的解；那当A[i]变成3的时候，A[j]我就可以从7位置向后找，不用再向前找。

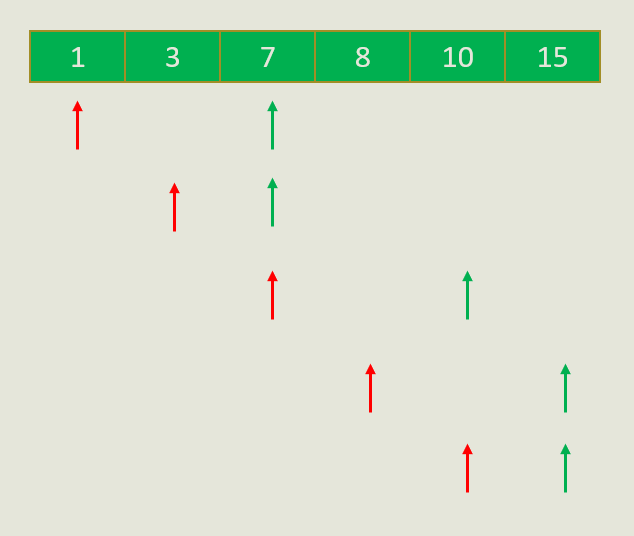
代码如下：

 1 #include <iostream>
 2 #include <algorithm>
 3 using namespace std;
 4 
 5 int main()
 6 {
 7     int n, k, min;
 8     int a[100000];
 9     
10     cin >> n >> k;
11     for(int i = 0; i < n; i ++)
12         cin >> a[i]; 
13     sort(a, a + n);        //递增排序
14     // 无解情况下
15     if(a[n-1] - a[0] < k )
16     {
17         cout << "no solution" << endl;
18         return 0;    
19     } 
20     //有解情况下
21     min = a[n-1] - a[0];
22     int j = 0;
23     for(int i = 0; i < n; i ++)
24     {
25         while( j <= n - 1 && a[j] - a[i] < k )
26             j ++;
27         if(a[j] - a[i] >= k && a[j] - a[i] < min)
28             min = a[j] - a[i];
29     }
30     cout << min << endl;
31     
32     return 0;
33 } 

第23~29行这部分的复杂度是O(N)。整体的时间复杂度由于前面有一个排序，所以是O(NlogN)。

双指针

标签：就是   tar   数量级   oop   需要   inter   course   双指针   ima   

原文地址：https://www.cnblogs.com/Tuple-Joe/p/9180529.html