Matlab filter常用函数

时间：2018-06-14 01:15:48 阅读：1500 评论：0 收藏：0 [点我收藏+]

标签：rip exp fun second type lower rand short function

Filtering and Analysis Functions

Filtering

Function	Description
`fftfilt`	Filters a signal with a `digitalFilter` using an FFT-based overlap-add method
`filter`	Filters a signal using a `digitalFilter`
`filtfilt`	Performs zero-phase filtering of a signal with a `digitalFilter`

Filter Analysis

Function	Description
`double`	Casts the coefficients of a `digitalFilter` to double precision
`filt2block`	Generates a Simulink? filter block corresponding to a `digitalFilter`
`filtord`	Returns the filter order of a `digitalFilter`
`firtype`	Returns the type (1, 2, 3, or 4) of an FIR `digitalFilter`
`freqz`	Returns or plots the frequency response of a `digitalFilter`
`fvtool`	Opens the Filter Visualization Tool and displays the magnitude response of a `digitalFilter`
`grpdelay`	Returns or plots the group delay response of a `digitalFilter`
`impz`	Returns or plots the impulse response of a `digitalFilter`
`impzlength`	Returns the length of the impulse response of a `digitalFilter`, whether actual (for FIR filters) or effective (for IIR filters)
`info`	Returns a character array with information about a `digitalFilter`
`isallpass`	Returns `true` if a `digitalFilter` is allpass
`isdouble`	Returns `true` if the coefficients of a `digitalFilter` are double precision
`isfir`	Returns `true` if a `digitalFilter` has a finite impulse response
`islinphase`	Returns `true` if a `digitalFilter` has linear phase
`ismaxphase`	Returns `true` if a `digitalFilter` is maximum phase
`isminphase`	Returns `true` if a `digitalFilter` is minimum phase
`issingle`	Returns `true` if the coefficients of a `digitalFilter` are single precision
`isstable`	Returns `true` if a `digitalFilter` is stable
`phasedelay`	Returns or plots the phase delay response of a `digitalFilter`
`phasez`	Returns or plots the (unwrapped) phase response of a `digitalFilter`
`single`	Casts the coefficients of a `digitalFilter` to single precision
`ss`	Returns the state-space representation of a `digitalFilter`
`stepz`	Returns or plots the step response of a `digitalFilter`
`tf`	Returns the transfer function representation of a `digitalFilter`
`zerophase`	Returns or plots the zero-phase response of a `digitalFilter`
`zpk`	Returns the zero-pole-gain representation of a `digitalFilter`
`zplane`	Displays the poles and zeros of the transfer function represented by a `digitalFilter`

1.zero,pole-->transfer function form

[b,a] = zp2tf(zer,pol,1);
fvtool(b,a)

技术分享图片

2.transform function-->zero/polo

fvtool(b,a,‘Analysis‘,‘polezero‘)

技术分享图片

zplane(b,a)

技术分享图片

3.Z-transform frequency response of a digital filter.

[h,w] = freqz(b,a,p)

returns the p-point complex frequency response, H(ejω), of the digital filter.

For example, a ninth-order Butterworth lowpass filter with a cutoff frequency of 400 Hz, based on a 2000 Hz sampling frequency, is

[b,a] = butter(9,400/1000);

To calculate the 256-point complex frequency response for this filter, and plot the magnitude and phase with freqz, use

freqz(b,a,256,2000)

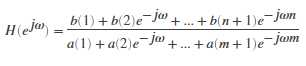
技术分享图片

4.filter

Use filter in the form y = filter(d,x) to filter an input signal, x, with a digitalFilter, d, and obtain output data, y.

5.designfilt(https://ww2.mathworks.cn/help/signal/ref/designfilt.html)

Use designfilt in the form d = designfilt(resp,Name,Value) to design a digital filter, d, with response type resp. Specify the filter further using a set of Name,Value pairs.

Type d.Coefficients to obtain the coefficients of a digitalFilter, d. For IIR filters, the coefficients are expressed as second-order sections.

Lowpass IIR Filter

Design a lowpass IIR filter with order 8, passband frequency 35 kHz, and passband ripple 0.2 dB. Specify a sample rate of 200 kHz. Visualize the magnitude response of the filter. Use it to filter a 1000-sample random signal.

lpFilt = designfilt(‘lowpassiir‘,‘FilterOrder‘,8, ...
         ‘PassbandFrequency‘,35e3,‘PassbandRipple‘,0.2, ...
         ‘SampleRate‘,200e3);
fvtool(lpFilt)

技术分享图片

dataIn = randn(1000,1);
dataOut = filter(lpFilt,dataIn);

Output the filter coefficients, expressed as second-order sections.

sos = lpFilt.Coefficients

sos = 4×6

    0.2666    0.5333    0.2666    1.0000   -0.8346    0.9073
    0.1943    0.3886    0.1943    1.0000   -0.9586    0.7403
    0.1012    0.2023    0.1012    1.0000   -1.1912    0.5983
    0.0318    0.0636    0.0318    1.0000   -1.3810    0.5090

Bandpass FIR Filter

Design a 20th-order bandpass FIR filter with lower cutoff frequency 500 Hz and higher cutoff frequency 560 Hz. The sample rate is 1500 Hz. Visualize the magnitude response of the filter. Use it to filter a random signal containing 1000 samples.

bpFilt = designfilt(‘bandpassfir‘,‘FilterOrder‘,20, ...
         ‘CutoffFrequency1‘,500,‘CutoffFrequency2‘,560, ...
         ‘SampleRate‘,1500);
fvtool(bpFilt)

技术分享图片

dataIn = randn(1000,1);
dataOut = filter(bpFilt,dataIn);

Output the filter coefficients.

b = bpFilt.Coefficients

b = 1×21

   -0.0113    0.0067    0.0125   -0.0445    0.0504    0.0101   -0.1070    0.1407   -0.0464   -0.1127    0.1913   -0.1127   -0.0464    0.1407   -0.1070    0.0101    0.0504   -0.0445    0.0125    0.0067   -0.0113 ?

6.fvtool

fvtool(b,a)
fvtool(sos)
fvtool(d)
fvtool(b1,a1,b2,a2,...,bN,aN)
fvtool(sos1,sos2,...,sosN)
fvtool(Hd)
fvtool(Hd1,Hd2,...,HdN)
h = fvtool(...)

Use fvtool to visualize a digitalFilter, d.

Matlab filter常用函数

标签：rip exp fun second type lower rand short function

原文地址：https://www.cnblogs.com/fellow1988/p/9180818.html

踩

(0)

评论一句话评论（0）

分享档案

更多>

2021年07月29日 (22)
2021年07月28日 (40)
2021年07月27日 (32)
2021年07月26日 (79)
2021年07月23日 (29)
2021年07月22日 (30)
2021年07月21日 (42)
2021年07月20日 (16)
2021年07月19日 (90)
2021年07月16日 (35)

周排行