标签:computer 距离 sample sep which multiple return img ef6
5 1 1 2 1 3 1 1 1Sample Output
3 2 3 4 4
题意 : 给你一颗树,以及树上两点之间的距离,求任意一点所能到的最远的距离。
思路分析:
对于这个问题,我们可以这样去思考,对于一颗树可以很方便的求出 以当前节点为根节点其所能到达的最远距离,但是这样并不能得到所有的节点的答案,其他的节点需要以其再考虑一下当前节点向上走的情况
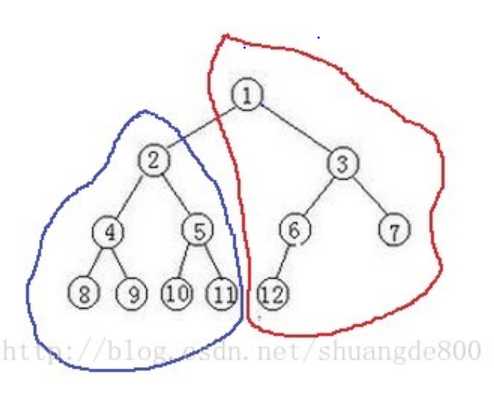
再考虑 2 这个节点的时候其最优值可能来自 2 这个子树,也可能来自于右侧的这颗红色的树,即向上走
dp[x][0] 表示 x 节点向下走的最大值, dp[x][1]表示 x 节点向下走的次大值, dp[x][2] 表示 x 节点向上走的最大值。
代码示例:
const int maxn = 1e4+5;
int n;
struct node
{
int to, cost;
node(int _to=0, int _cost=0):to(_to), cost(_cost){}
};
vector<node>ve[maxn];
int dp[maxn][3];
int p[maxn];
void dfs1(int x, int fa){
for(int i = 0; i < ve[x].size(); i++){
int to = ve[x][i].to;
int cost = ve[x][i].cost;
if (to == fa) continue;
dfs1(to, x);
if (dp[x][0] <= dp[to][0]+cost){
dp[x][1] = dp[x][0];
dp[x][0] = dp[to][0]+cost;
p[x] = to;
}
else if (dp[x][1] < dp[to][0]+cost){
dp[x][1] = dp[to][0]+cost;
}
}
}
void dfs2(int x, int fa){
for(int i = 0; i < ve[x].size(); i++){
int to = ve[x][i].to;
int cost = ve[x][i].cost;
if (to == fa) continue;
if (to != p[x]){
dp[to][2] = max(dp[x][0]+cost, dp[x][2]+cost);
}
else dp[to][2] = max(dp[x][1]+cost, dp[x][2]+cost);
dfs2(to, x);
//printf("++++ %d %d %d \n", x, to, dp[to][2]);
}
}
int main() {
//freopen("in.txt", "r", stdin);
//freopen("out.txt", "w", stdout);
int x, y;
while(~scanf("%d", &n)){
for(int i = 1; i <= n; i++) ve[i].clear();
for(int i = 2; i <= n; i++){
scanf("%d%d", &x, &y);
ve[i].push_back(node(x, y));
ve[x].push_back(node(i, y));
}
memset(dp, 0, sizeof(dp));
dfs1(1, 0);
dfs2(1, 0);
for(int i = 1; i <= n; i++) {
printf("%d\n", max(dp[i][0], dp[i][2]));
}
}
return 0;
}
标签:computer 距离 sample sep which multiple return img ef6
原文地址:https://www.cnblogs.com/ccut-ry/p/9188796.html