数据结构：图

标签：tac   解决   str   mes   span   初始   bre   答案   搜索   

1.学习总结

（1）掌握图的相关概念，包括图、有向图、无向图、完全图、子图、连通图、度、入度、出度、简单回路和环等定义。

（2）重点掌握图的各种存储结构，包括邻接矩阵和邻接表等。

（3）重点掌握图的基本运算，包括创建图、输出图、深度优先遍历、广度优先遍历等。

（4）掌握图的其他运算，包括最小生成树、最短路径、拓扑排序和关键路径等的算法。

（5）灵活运用图这种数据结构解决一些综合应用问题。

1.1图的思维导图

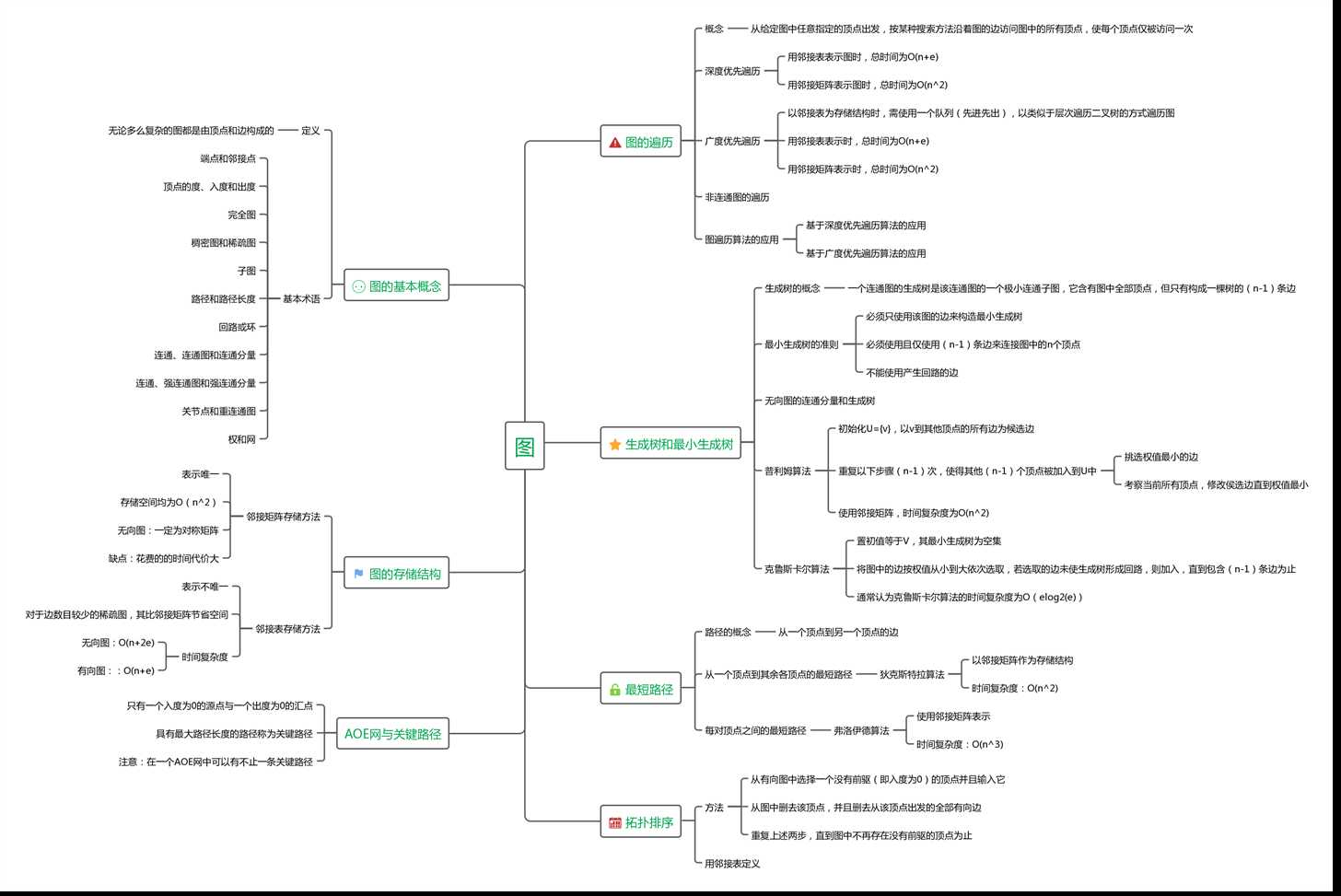
1.2图结构学习体会

• 深度遍历算法：一条路走到底，没路时再返回上一个找其他路，循环操作到遍历完所有顶点为止。
• 广度遍历算法：先输出与首个顶点有路的所有顶点，再按先进先出法则输出与该顶点有路的顶点。
• Prim和Kruscal算法：均为求最小生成树的算法，前者时间复杂度为O(n^2),后者为O(elog2(e))。
• Dijkstra算法：以邻接矩阵作为存储结构，其算法时间复杂度为O(n^2)。
• 拓扑排序算法：有向图，用邻接表定义，从入度为0的点出发走到没有前驱的顶点。

2.PTA实验作业

2.1.1题目1：图着色问题

2.1.2设计思路

直接用图的遍历，遍历的时候判断是否颜色相等即可。任选一顶点着色1，在图中尽可能多的用颜色1着色，当不能用颜色1着色时，转用其他颜色，直到所有顶点都被着色为止。（PS：伪代码思路为最初思路，实际代码已经修改成更精简的方法）

伪代码：

while each vertex in G 初始化颜色为0

vertex[0]=1//选初始点颜色置为1

置颜色种类color=0；

循环置所有顶点着色

  color++;//取下一颜色

  while each vertex in G

     if vertex[i]已着色，转下一顶点

     else

         若该点用color着色与其他邻接点颜色不冲突

         vertex[i]=color;

         否则不着色

2.1.3代码截图

2.1.4PTA提交列表说明

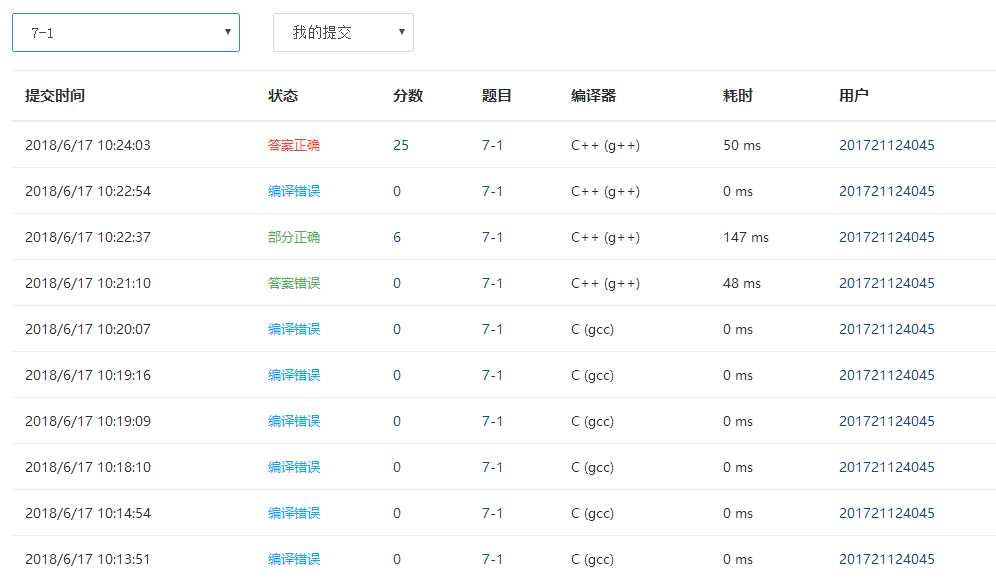
 开始的多次编译错误是因为代码使用的是C++，而PTA的初始编译器是C（gcc），经发现并改正后得以解决。答案错误是因为没有按照格式输出，部分正确是因为对题目的多种情况考虑不全，几经修改，最后答案正确。

2.2.1题目2：排座位

2.2.2设计思路

假设俩人A和B，需考虑如下情况：

（1） 如果A、B是直接的朋友，输出 No problem 
（2）否则如果A、B不敌对，输出OK 
（3）否则如果A、B敌对但他们有共同的朋友，输出OK but... 
（4）否则A、B敌对并且没有共同的朋友，输出No way

2.2.3代码截图

2.2.4PTA提交列表说明

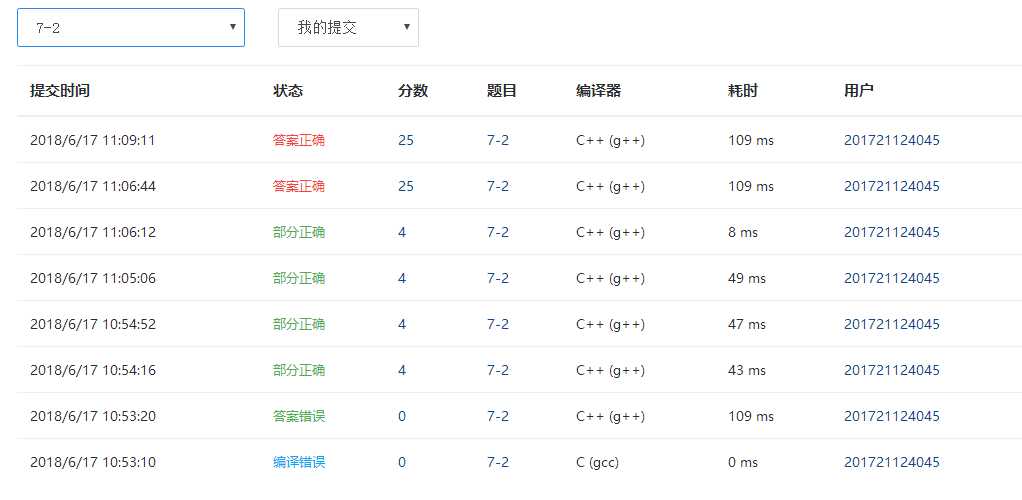
开始的编译问题依然是编译器的选择问题，随后的答案错误是因为输出格式没有严格按照要求，紧接着的多次部分正确是因为题目的多种情况没整理完全，经一步步的完善后答案正确。

2.3.1题目3：六度空间

2.3.2设计思路

该题主要是解决超时的问题卡的比较久。 
比如像visited[]，不是简单的0.1定义，不然每对一个数字进行遍历都还要重置visited[]。

2.3.3代码截图

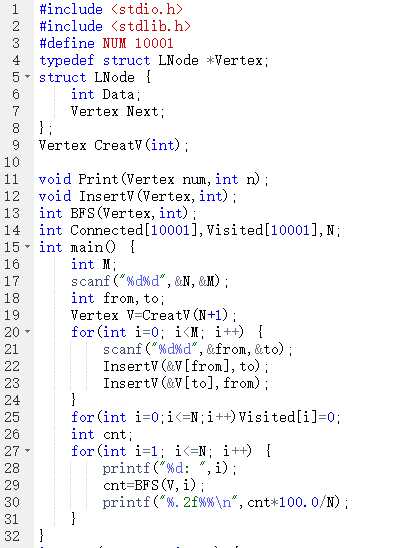
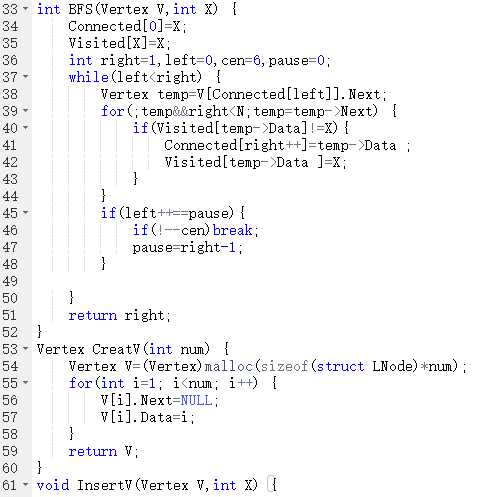
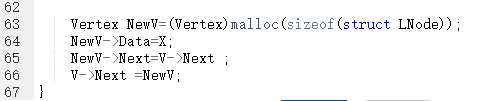
2.3.4PTA提交列表说明

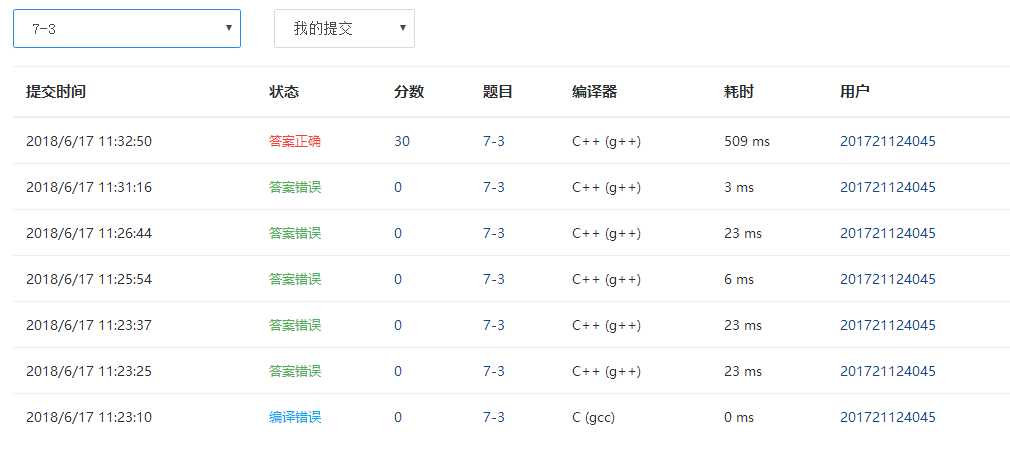
编译错误依旧是编译器的选择问题，多次答案错误是因为没有深入理解题意，以致于错漏百出，几番周折后答案正确。

3.本周PTA题目集最后排名截图

本次题目集总分：135分（时间：2018/6/17 13：12）

3.1PTA排名

47

3.2我的总分

135

4.阅读代码

 天梯地图代码阅读：

最短路，麻烦的是多条最短路中推荐最优的路线，并输出路径。路径的还原可以不断记录前驱节点，注意的是每个节点的前驱节点可能不止一个，全需要记录，最后搜索最优路径。

1. #include <iostream> 
2. #include <cstdio>  
3. #include <cstdlib>  
4. #include <cstring>  
5. #include <string>  
6. #include <algorithm>  
7. #include <cmath>  
8. #include <map>  
9. #include <queue>  
10. #include <stack>  
11. #include <set>  
12. using namespace std;  
13. const int INF = 0x3f3f3f3f;  
14. const int maxn = 1e4+10;  
15. /*----------------------------------------------------------------head------------------------------------------------------------------*/  
16. int n,m,ss,dd;  
17. int T[510][510],D[510][510],dist[510],disd[510],vist[510],visd[510],pret[510]/*记录最小时间的前驱*/,pred[510]/*记录最短距离的前驱*/,SUM[510]/*记录节点个数*/;  
18. int u,v,is,d,t;  
19. void print(int cnt,int c[]){//打印路径  
20.     for(int i = cnt-1; i >= 0; i--){  
21.         if(i != cnt-1)  
22.             printf(" =>");  
23.         printf(" %d",c[i]);  
24.     }  
25.     puts("");  
26. }  
27. /*------------------------------------------------------------dijkstra-----------------------------------------------------------------*/  
28. //求解最小时间的最短路  
29. void dijkstraT(){  
30.     for(int i = 0; i < n; i++){//初始化  
31.         dist[i] = T[ss][i];  
32.         disd[i] = D[ss][i];  
33.         vist[i] = visd[i] = 0;  
34.         pret[i] = pred[i] = ss;  
35.     }  
36.     dist[ss] = disd[ss] = 0;//初始化  
37.     vist[ss] = visd[ss] = 1;//初始化  
38.     pret[ss] = -1;//初始化  
39.     int Min,pos;  
40.     for(int i = 1; i < n; i++){  
41.         Min = INF;  
42.         for(int j = 0; j < n; j++){  
43.             if(!vist[j] && dist[j]<Min){  
44.                 Min = dist[j];  
45.                 pos = j;  
46.             }  
47.         }  
48.         vist[pos] = 1;  
49.         for(int j = 0; j < n; j++){  
50.             if(!vist[j] && dist[j]>dist[pos]+T[pos][j]){  
51.                 dist[j] = dist[pos]+T[pos][j];  
52.                 disd[j] = disd[pos]+D[pos][j];  
53.                 pret[j] = pos;  
54.             }  
55.             else if(!vist[j] && dist[j] == dist[pos]+T[pos][j]){  
56.                 if(disd[j] > disd[pos]+D[pos][j]){//时间相同选距离最短  
57.                     disd[j] = disd[pos]+D[pos][j];  
58.                     pret[j] = pos;  
59.                 }  
60.             }  
61.         }  
62.     }  
63. }  
64. //求解最短距离的最短路  
65. void dijkstraD(){  
66.     for(int i = 0; i < n; i++){//初始化  
67.         disd[i] = D[ss][i];  
68.         visd[i] = 0;  
69.         pred[i] = ss;  
70.         SUM[i] = 1;  
71.     }  
72.     disd[ss] = 0;//初始化  
73.     visd[ss] = 1;//初始化  
74.     pred[ss] = -1;//初始化  
75.     int Min,pos;  
76.     for(int i = 1; i < n; i++){  
77.         Min = INF;  
78.         for(int j = 0; j < n; j++){  
79.             if(!visd[j] && disd[j]<Min){  
80.                 Min = disd[j];  
81.                 pos = j;  
82.             }  
83.         }  
84.         visd[pos] = 1;  
85.         for(int j = 0; j < n; j++){  
86.             if(!visd[j] && disd[j]>disd[pos]+D[pos][j]){  
87.                 disd[j] = disd[pos]+D[pos][j];  
88.                 pred[j] = pos;  
89.                 SUM[j] = SUM[pos]+1;  
90.             }  
91.             else if(!visd[j] && disd[j]==disd[pos]+D[pos][j]){//距离相同选节点数最小  
92.                 if(SUM[j] > SUM[pos]+1){  
93.                     SUM[j] = SUM[pos]+1;  
94.                     pred[j] = pos;  
95.                 }  
96.             }  
97.         }  
98.     }  
99. }  
100. /*------------------------------------------------------------main--------------------------------------------------------------------*/  
101. int main(){  
102.     scanf("%d %d",&n,&m);  
103.     memset(T,INF,sizeof(T));  
104.     memset(D,INF,sizeof(D));  
105.     while(m--){  
106.         scanf("%d %d %d %d %d",&u,&v,&is,&d,&t);  
107.         if(is){  
108.             if(T[u][v]>t)//去重  
109.                 T[u][v] = t;  
110.             if(D[u][v]>d)//去重  
111.                 D[u][v] = d;  
112.         }  
113.         else{  
114.             if(T[u][v]>t)//去重  
115.                 T[u][v] = T[v][u] = t;  
116.             if(D[u][v]>d)//去重  
117.                 D[u][v] = D[v][u] = d;  
118.         }  
119.     }  
120.     scanf("%d %d",&ss,&dd);  
121.     dijkstraT();  
122.     dijkstraD();  
123.     int pt = dd;  
124.     int pd = dd;  
125.     int flag = 1;//flag==1表示两条路径相同，不然不同。  
126.     int a[510],b[510],cnta,cntb;  
127.     cnta = cntb = 0;  
128.     while(pt != -1){  
129.         a[cnta++] = pt;  
130.         pt = pret[pt];  
131.     }  
132.     while(pd != -1){  
133.         b[cntb++] = pd;  
134.         pd = pred[pd];  
135.     }  
136.     if(cnta != cntb)//节点数不同路径肯定不同  
137.         flag = 0;  
138.     else{  
139.         for(int i = 0; i < cnta; i++){  
140.             if(a[i] != b[i]){  
141.                 flag = 0;  
142.                 break;  
143.             }  
144.         }  
145.     }  
146.     if(flag){  
147.         printf("Time = %d; Distance = %d:",dist[dd],disd[dd]);  
148.         print(cnta,a);  
149.     }  
150.     else{  
151.         printf("Time = %d:",dist[dd]);  
152.         print(cnta,a);  
153.         printf("Distance = %d:",disd[dd]);  
154.         print(cntb,b);  
155.     }  
156.     return 0;  
157. }  

数据结构：图

标签：tac   解决   str   mes   span   初始   bre   答案   搜索   

原文地址：https://www.cnblogs.com/999ganmaoling/p/9191389.html