Fibonacci series(斐波纳契数列)的几种常见实现方式

标签：fibonacci   算法   

费波那契数列的定义：

费波那契数列（意大利语：Successione di Fibonacci），又译费波拿契数、斐波那契数列、斐波那契数列、黄金分割数列。

在数学上，费波那契数列是以递归的方法来定义：

• 
• 
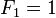
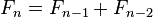• (n≧2)

用文字来说，就是费波那契数列由0和1开始，之后的费波那契系数就由之前的两数相加。

首几个费波那契系数是：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233……

特别指出：0不是第一项，而是第零项。

下面是费波那契数列的几种常见编程实现：

1、常规实现：

int Fibonacci(int n)
{
	int a = 1, b = 1;
	if(n < 0)
	{
		printf("The fibonacci number exists only with nonnegative index.\n");
		return -1;
	}
	else if (n == 0)
		return 0;
	else if(n==1 || n==2)
		return 1;
	else
	{
		for(int i=3; i<=n; i++)
		{
			int tmp = b;
			b = a + b;
			a = tmp;
		}
		return b;  
	}
}

2、递归实现：

int Fibonacci(int n)
{
	if(n < 0)
		printf("The fibonacci number exists only with nonnegative index.\n");
	else
	{
		if(n == 0)
			return 0;
		else if(n == 1)
			return 1;
		else
			return Fibonacci(n - 1) + Fibonacci(n - 2);
	}
}

3、迭代实现：

int Fibonacci_iter(int a, int b, int count)
{
	if(count < 0)
		printf("The fibonacci number exists only with nonnegative index.\n");
	else if(count == 0)
		return b;
	else
		return Fibonacci_iter(a + b, a, count - 1);
}

int Fibonacci(int n)
{
	return Fibonacci_iter(1, 0, n);
}

#include<iostream>

using namespace std;

int Result;

//主模板
template<int N> //模板
class Fibonacci
{
public:
	enum{Result = Fibonacci<N-1>::Result + Fibonacci<N-2>::Result };   //枚举，带有隐含计算
};

//完全特化模板
template<>
class Fibonacci<1> //带常参数1的构造函数
{
public:
	enum { Result = 1 };   //给枚举赋初值1
};

//完全特化模板
template<>
class Fibonacci<0> //带参数0的模板
{
public:
	enum { Result = 0 };   //给枚举赋初值0
};

int main()
{
	std::cout << "第20项的Fibonacci数是：" << Fibonacci<20>::Result << std::endl;   //隐含计算
	system("pause");
	return 1;
}

Fibonacci series(斐波纳契数列)的几种常见实现方式

标签：fibonacci   算法   

原文地址：http://blog.csdn.net/usstmes318/article/details/39667363