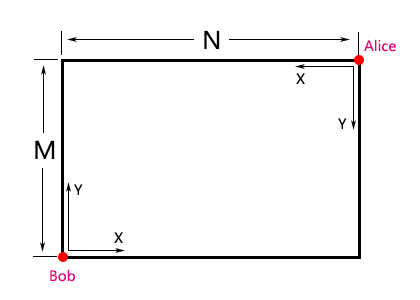
10 10 5 5 10 10 6 6
YES NO
#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=100010;
typedef long long ll;
int main()
{
int n,m,x,y;
while(~scanf("%d%d%d%d",&n,&m,&x,&y))
{
if(x==n-x&&y==m-y)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}3 0 1 3 3 5 4 2 3 2 4 6
301 425 -1
#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=100010;
typedef long long ll;
int arr[150],brr[150];
int main()
{
int n,i,p,ct;
while(~scanf("%d",&n))
{
ct=0,p=-1;
for(i=0;i<n;i++)
{
scanf("%d",&arr[i]);
if(arr[i]&1)
{
if(p==-1||arr[i]<arr[p])
p=i;
}
}
if(p==-1)
{
printf("-1\n");
continue;
}
for(i=0;i<n;i++)
if(i!=p)
brr[ct++]=arr[i];
sort(brr,brr+ct);
if(ct&&brr[ct-1]==0)
{
printf("-1\n");
continue;
}
for(i=ct-1;i>=0;i--)
printf("%d",brr[i]);
printf("%d\n",arr[p]);
}
return 0;
}
3 abc 1 abcabc 1 abcabc 2
6 15 21
#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=100002;
typedef long long ll;
char txt[maxn];
int vis[27];
ll ans=0;
int main()
{
int t,n,k,le,ri,p;
scanf("%d",&t);
while(t--)
{
scanf("%s%d",txt,&k);
n=strlen(txt);
ans=le=ri=0;
memset(vis,0,sizeof vis);
p=-1;
while(ri<=n)
{
if(p==-1)
{
vis[txt[ri]-'a']++;
if(vis[txt[ri]-'a']>k)
p=ri;
else if(ri<n)
ans+=ri-le+1;
ri++;
}
else
{
vis[txt[le]-'a']--;
if(txt[le]==txt[p])
p=-1,ans+=ri-le-1;
le++;
}
}
printf("%I64d\n",ans);
}
return 0;
}
1 5 7 10 11 12 13 14 Q 1 5 2 1 Q 1 5 1 0 Q 1 5 1 1 Q 1 5 3 0 Q 1 5 3 1 S 1 100 Q 1 5 3 1
5 1 1 5 0 1
#include<algorithm>
#include<iostream>
#include<string.h>
#include<stdio.h>
#include<math.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=100003;
typedef long long ll;
#define lson L,mid,ls
#define rson mid+1,R,rs
int val[maxn][11],da[400][11][10],x;
int main()
{
int t,n,m,i,j,le,ri,d,p,x,y,bk,ans,st,ed,lim;
char cmd[10];
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&m);
bk=ceil(sqrt(1.0*n));
memset(da,0,sizeof da);
memset(val,0,sizeof val);
for(i=1;i<=n;i++)
{
scanf("%d",&x);
for(j=1;j<=10;j++)
{
val[i][j]=x%10;
x/=10;
}
p=(i-1)/bk;
for(j=1;j<=10;j++)
da[p][j][val[i][j]]++;
}
for(i=0;i<m;i++)
{
scanf("%s",cmd);
if(cmd[0]=='Q')
{
scanf("%d%d%d%d",&le,&ri,&d,&p);
ans=0;
st=(le-1)/bk;
ed=(ri-1)/bk;
if(ed-st<=1)
{
for(j=le;j<=ri;j++)
if(val[j][d]==p)
ans++;
}
else
{
lim=(st+1)*bk;
for(j=le;j<=lim;j++)
if(val[j][d]==p)
ans++;
lim=ed*bk+1;
for(j=lim;j<=ri;j++)
if(val[j][d]==p)
ans++;
for(j=st+1;j<ed;j++)
ans+=da[j][d][p];
}
printf("%d\n",ans);
}
else
{
scanf("%d%d",&x,&y);
p=(x-1)/bk;
for(j=1;j<=10;j++)
{
if(y%10!=val[x][j])
{
da[p][j][val[x][j]]--;
val[x][j]=y%10;
da[p][j][val[x][j]]++;
}
y/=10;
}
}
}
}
return 0;
}
BestCoder Round #11 (Div. 2)题解集合
原文地址:http://blog.csdn.net/bossup/article/details/39665795