标签:.com 构造 说明 而且 矩阵 聚合 完整 规则 构造矩阵
初看闭包,闭包可以被理解为,一组元素通过一些关系聚合在一起,而且这些关系已经是这些元素之间所有的关系了。
这些元素动用所有的关系,去找和其存在这种关系的其他元素。再将找到的这些元素并入集合中去,直到不能在发现新的元素为止。更形象的来说就是使用现有集合内的元素的所有关系进行扩充,像"滚雪球"一般的不断扩充。直至没法再吸收新的元素进入。
属性闭包正是使用属性间的函数依赖进行滚雪球的过程。
对于属性闭包 首先要了解阿姆斯特朗公理

阿姆斯特朗公理是讲述属性间的函数依赖关系,可以通过这些公理进行拓展。

选定一个元素X作为起点,用所关联的函数依赖+阿姆斯特朗扩展的函数依赖关系不断滚雪球得到的集合中的所有属性,正是属性闭包。

计算方面如图所示,正是经过一系列滚雪球般的操作,使之到达不变为止。
最小覆盖的定义及算法

再将所有函数依赖的右部都分解成只有一个属性后,进行枚举测试,尝试剔除每一个元素,判断把该元素剔除掉之后,新的集合是否与旧集合等价。

生成最小覆盖的算法就是逐一枚举并判读,没有什么好办法
模式分解无损性及其检查
定义

分解后的各个关系按照其所有属性连接起来再投影后,其结果与原来的关系等价,即没有函数依赖关系或者是数据被丢失掉。
模式分解完整性检查
有以下算法:
第一步构造矩阵:
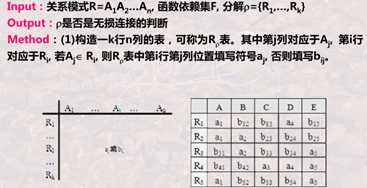
记录各个子关系中,所包含的属性情况,如果包含该属性 记为 a列数
不包含则记为 b行数列数
第二步遍历所有关系,开始对表进行修改:规则如下

在列上找在依赖关系左边X的那几列,如果这几列中的行中存在相同值的个数大于一个的行,将其依赖右侧Y的列的对应的行的内容进行更改。
更改规则如上,有a优先置a,无a则任选一个b就行。
验证方法:
遍历完所有的依赖关系后,修改完成后的表如果存在一行全为a,说明分解无损

如果分解后的关系只有两个关系,可以用这个方法简单判断:

标签:.com 构造 说明 而且 矩阵 聚合 完整 规则 构造矩阵
原文地址:https://www.cnblogs.com/scarecrow-ryan/p/9206415.html