标签:als == 表操作 存储结构 作用 长度 typedef 频繁 计数器
在生活中其实处处可见线性表的例子。比如一个班级的小朋友,一个跟着一个排着队,有一个打头,有一个收尾,当中的小朋友 每一个都知道他前面一个是谁,他后面一个是谁,这样如同有一根线把他们串联起来 了。 就可以称之为线性表。
所以线性表的定义为:零个或多个数据元素的有限序列。
首先它是一个序列。 也就是说,元素之间是有顺序的,若元素存在多个,则第一 个元素无前驱,最后一个元素无后继,其他每个元素都有且只有一个前驱和后继。 然后,线性表强调是有限的,小朋友班级人数是有限的,元素个数当然也是有限的。
那么定义好的线性表应该具有哪些操作呢?还是以前面排好队的小朋友举例子,我们可以知道这个队伍的长度,也可以找出队伍里的某个小朋友,有时我们还需要知道队伍里有没有一个叫小明的同学,这种查找某个元素是否存在也是线性表的必要操作。对于一个幼儿园来说,加入一个新的小朋友到队列中,或因某个小朋友生病,需要移除某个位置,也是很正常的情况,因此对于一个线性表来说,插入数据和删除数据都是必须的操作。所以我们可以定义这样一个线性表的抽象数据类型。
类型名称:线性表(List) 数据对象集:线性表是 n (≥0)个元素构成的有序序列( a1, a2, ...,an ) 操作集:线性表L List,整数i表示位置,元素X ? ElementType, 线性表基本操作主要有: 1、List MakeEmpty():初始化一个空线性表L; 2、ElementType GetElem( int K, List L ):根据位序K,返回相应元素 ; 3、int Find( ElementType X, List L ):在线性表L中查找X的第一次出现位置; 4、void Insert( ElementType X, int i, List L):在位序i前插入一个新元素X; 5、void Delete( int i, List L ):删除指定位序i的元素; 6、int Length( List L ):返回线性表L的长度n
线性表这种有限序列的逻辑结构我们怎样在计算机中以物理形式存储起来呢?我们有两种实现方式:顺序存储和链式存储。
线性表的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。
#include<stdio.h> //宏定义 #define MAXSIZE 50 //存储空间初始量分配 #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0
typedef int Status; typedef int ElemType;//定义int类型的别名为ElemType //初始化一个线性表结构体 typedef struct { ElemType data[MAXSIZE];//数组存储数据元素,最大值为MAXSIZE int length;//线性表当前长度 }SqList; //获取线性表L中的第i个元素,并传给变量e, Status GetElem(SqList L,int i,*e){ if(L.length==0 || i<1 || i>L.length){ return ERROR; } *e = L.data[i-1]; return OK; } //在L中的第i个位置插入一个元素e Status InsertList(SqList *L,int i,ElemType e){ //SqList *L;定义一个指向线性表地址的指针变量L int k; if(L->length==MAXSIZE){ return ERROR;//线性表已满 } if(i<1 || i>L->length){ return ERROR;//插入的位置不对 } for(k=L->length-1;k>=i-1;k--){ L->data[k+1] = L->length[k]; } L->length[i-1]=e;//将新元素插入 L->length++;//线性表长度加1 return OK; } //删除L中的第i个元素,并用变量e返回其值 Status ListDlelte(SqList *L,int i,ElemType *e){ int k; if(L->length == 0 || L->length == MAXSIZE){ //线性表为空或已满 return ERROR; } if(i<1 || i>L->length){ return ERROR; } *e = L->data[i-1]; for(k=i;k>L->length;k++){ L->data[k-1] = L->data[k]; } L->length--; return OK; }
线性表的顺序存储结构,在读数据时,不管是哪个位置,时间复杂度都是 0(1); 而插入或删除时,时间复杂度都是 O(n)。这就说明 ,它比较适合元 素个数不大变化,而更多是存取数据的应用。顺序存储的优缺点有。
| 优点 | 缺点 |
| 无须为表示表中元素之 间的逻辑关系而增加额 外的存储空间 | 插入和删除需要移动大量元素 |
| 可以快速的存取表中任意位置的元素 | 当线性表长度变化较大时,难以确定存储空间的容量,造成存储空间的碎片 |
既然顺序存储因为其插入和删除元素需要移动大量的元素而造成时间性能上的浪费。那么有没有一种存储结构能弥补顺序存储结构的缺点呢。当然是有的,就是我们接下来要讲的链式存储结构。
和顺序存储不同的是,链式存储不需要向顺序存储那样开辟一块连续的存储空间来存储线性表元素,而是分散的插入到空闲的内存空间中。这样的话,前面的元素如果找到后面的元素就需要知道后一个元素的地址。因此链式存储的线性表结点就由两部分信息组成(存储数据元素信息的数据域和存储后继结点地址的指针域)。链表中的每个结点都存有一个指针域,因此也称作单链表。
#include<stdio.h> typedef int ElemType typedef int Status #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 /* 单链表结点存储结构 */ typedef struct Node{ ElemType data; //定义一个整型变量data struct Node *next;//定义一个结构体的指针变量 }Node;
单链表的结点定义好了,那么我们如何来遍历单链表的每一个结点元素呢?
既然元素结点的指针域存储了后继元素的地址,这样的话我们就可以定义一个指针变量来遍历所有的结点元素。
typedef struct Node *LinkList; //定义指向单链表结点结构的指针变量,别名为LinkList
我们 假设p 是指向钱性表第 i 个元素的指针,则该结点 aj 的数据域 我们可以用 p->由回 来表示, p->由恒的值是一个数据元素,结点 aj 的指针域可以用 p->next 来表示, p->next 的值是一个指针。 p->next 指向谁呢? 当然是指向第 i+l 个 元素,即指向 ai+1 的指针。
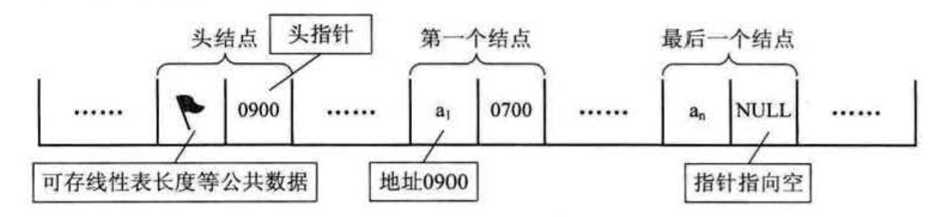
所以线性表的链表操作定义为
//获取单链表中的第i个元素 Status GetElem(LinkList L,int i,ElemType *e){ int j; LinkList p; //声明一个结构体指针变量p p = L->next;//让p指向链表L的第一个节点 j = 1; //j为计数器 while(p && j<i){ p = p->next; //让p指向下一个节点 j++; } if(!p || j>i){ return ERROR; } *e = p->data; return OK; } //在L中第i个位置之前插入新的数据元素e,L的长度增加1 Status ListInsert(LinkList *L,int i,ElemType e){ int j; LinkList p,s; p = *L;//指针变量p的作用是遍历单链表 j = 1; while(p && j<i){ //寻找第i个节点 p = p->next; j++; } if(!p || j>i){ return ERROR; } s = (LinkList)malloc(sizeof(Node));//创建一个存放指针变量的新结点 s->data = e; s->next = p->next; p->next = s; *L->length++; return OK; } //删除L中的第i个数据元素,并用e返回其值, L的长度减1 Status ListDelete(LinkList *L,int i,ElemType *e){ int j; LinkList p,q; p = *L; j = 1; while(p->next && j<i){ //遍历寻找第i个元素 p = p->next; j++; } if(!(p->next) || j>i){ return ERROR; //第i个元素不存在 } q = p->next; p->next = q->next; *e = q->data; *L->length--; free(q); return OK; }
线性表的链式存储结构,在读数据时,由于后继元素只能通过前驱元素的指针来访问,所以时间复杂度是 O(n); 而插入或删除时,要先遍历再插入或删除,遍历的复杂度为O(n),插入或删除的时间复杂度是 O(1)。这就说明 ,它比较适合元需要频繁插入或删除元素的应用。
| 顺序存储 | 链式存储 | |
| 查找(时间性能) | O(1) | O(n) |
| 插入和删除(时间性能) | 顺序存储结构需要移动表长一半的元素, 时间为O(n) |
单链表在找出某位置的指针后,插入和删除间仅为O(1) |
| 空间性能 | 服序存储结构需要预先分配内存,分大了浪费, 分小了易发生上溢 |
单链表不需要预先分配存储空间,只要有就可以分配, 元素个数也不受限制 |
标签:als == 表操作 存储结构 作用 长度 typedef 频繁 计数器
原文地址:https://www.cnblogs.com/yuliangbin/p/8761658.html