2.2 与球体相交-几何解

标签：避免   停止   情况下   允许   地方   计算   http   外部   精度   

　　现在，一个简单的球体相交例子已经被概述。这里有一些关于计算效率的概念。

　　一个普遍的看法是，应该尽可能地避免使用平方根函数。检查计时：sqrt()耗时通常是乘法的15~30倍。类似的，除法比乘法耗时更长，所以除法可以用乘以逆来代替。

　　另一个观察的结果是，计算往往会被缩短。在球体情况下，许多测试检测了球体相交问题，这些测试的目的是避免非必要的计算。

　　通过研究几何，问题的其他性质就变得明了了。

　　例如，光线通常指向球外，这种不相交。通过研究这个可能，我们发现了另一种测试光线和球面相交的策略。

　　　　1) 找出光线原点是否在球面外

　　　　2) 找出光线最接近球体中心的地方

　　　　3) 如果光线在球体外且指向远离球的方向，那么光线一定会错过球体

　　　　4) 另外，求出离球体面最近的距离的平方

　　　　5) 如果值为负，光线会错过球面

　　　　6) 另外，从上面找出射线/表面距离

　　　　7) 计算触点坐标[x_i y_i z_i]

　　　　8) 计算交点法线

　　该策略将方程(A5)和(A6)分解成更短的表达式，并根据需要进行计算。条件3,5将检测射线偏离球面状况。并允许提前停止。

　　以上内容将被充实和解释。从原始的射线(A1)和球面(A2)方程开始。首先，通过计算确定光线的来源是否在球内。

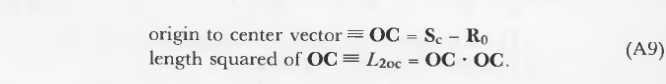
　　如果L_2oc<S_r²，则光源在球内。若L_2oc>=S_r²，则光源点在球外或者球内。然后有可能不与球相交。效率起见，可以提前计算并保存S_r²

　　注意，起源于球体的光线不算集中球体。这是ray tracing的标准，反击和折射来自之前的相交处。在"精度问题"章节会讨论如何规避。

　　在任何情况下，下一步都是计算球心到离他最近的线点的距离。这就等于求出射线与垂直于它的平面(穿过球心)的交点。

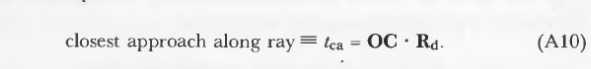
　　t_ca<0，光线在球后。对于来自外部的光线，这意味着光线不能击中球体，另一种说法是，t_ca<0，射线指向原理球心，如图2

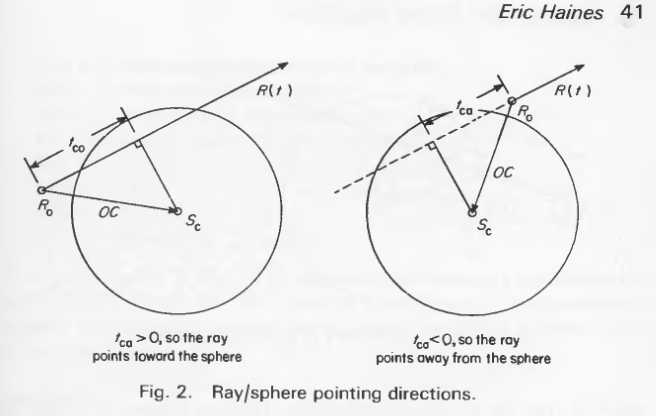
　　一旦t_ca确定，从垂直点到球面的距离也就确定了。

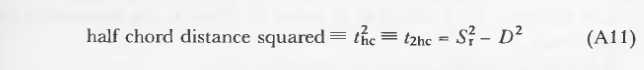
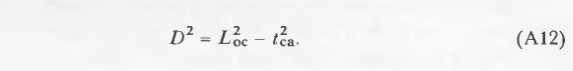
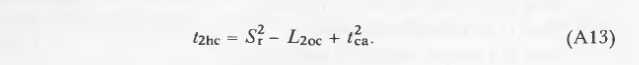
　　方程的几何意义展示在图3.这个计算引出了另一个关于关于光线是否击中球体的测试。如果t2hc<0，光线会错过球面，当然，以上都是建立在光源不在球内的基础上。

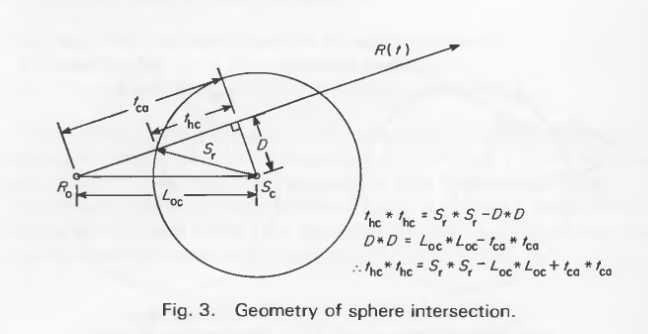
　　使用A7,A8之前会使用到前面的方程。

　　总结：

　　　　1，找出球心到光源的距离

　　　　2，找出球心最近的光源上的点

　　　　3，测试光线是否在球外且指向球外

　　　　4，找出thc

　　　　5，判断thc2是否为负

　　　　6，计算交距t

　　　　7，找出交点

　　　　8，计算交点和法线

2.2 与球体相交-几何解

标签：避免   停止   情况下   允许   地方   计算   http   外部   精度   

原文地址：https://www.cnblogs.com/TooYoungTsukasa/p/9211218.html