标签:class pac 基础 图片 TE read etc har +=
小 C 最近学了很多最小生成树的算法,Prim 算法、Kurskal 算法、消圈算法等等。 正当小 C 洋洋得意之时,小 P 又来泼小 C 冷水了。小 P 说,让小 C 求出一个无向图的次小生成树,而且这个次小生成树还得是严格次小的,也就是说: 如果最小生成树选择的边集是 EM,严格次小生成树选择的边集是 ES,那么需要满足:(value(e) 表示边 e的权值) 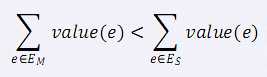
这下小 C 蒙了,他找到了你,希望你帮他解决这个问题。
第一行包含两个整数N 和M,表示无向图的点数与边数。 接下来 M行,每行 3个数x y z 表示,点 x 和点y之间有一条边,边的权值为z。
包含一行,仅一个数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
11
数据中无向图无自环; 50% 的数据N≤2 000 M≤3 000; 80% 的数据N≤50 000 M≤100 000; 100% 的数据N≤100 000 M≤300 000 ,边权值非负且不超过 10^9 。
实际上你要先求出最小生成树,然后再在这个基础上改一点点就变成了次小生成树。
具体来说就是找一条以前没有用的边,然后把这两点原来路径上的一条最大的边给砍了。。。
然后题目很变态的要求严格小于。。。你还要记第二小的边。。。。
最开始偷懒用set。。。被卡常了。。。
然后最后4分钟卡常大师重出江湖。。。。一手sort直接*过。。。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
struct lpl{
int from, to, dis;
bool flag;
}lin;
struct ld{
int to, dis;
}qwe;
struct lpd{
int fa, dis, deep, tree[18][3];
}node[maxn];
int n, m, root, pw[25], fa[maxn];
int tot, aaa[maxn];
long long sum = 0, ans = 1e14 + 5;
set<int> s;
set<int>::iterator iter;
vector<lpl> edge;
vector<ld> point[maxn];
inline int read()
{
int s = 0, w = 1; char ch = getchar();
while(ch <= '0' || ch > '9'){if(ch == '-') w = -1; ch = getchar();}
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
inline bool cmp(lpl A, lpl B){return A.dis < B.dis;}
int find(int t){return t == fa[t] ? t : fa[t] = find(fa[t]);}
inline void putit()
{
n = read(); m = read(); root = 1; pw[0] = 1;
for(int a, b, i = 1; i <= m; ++i){
scanf("%d%d%d", &lin.from, &lin.to, &lin.dis); edge.push_back(lin);
}
for(int i = 1; i <= 17; ++i) pw[i] = pw[i - 1] * 2;
}
inline void kruskal()
{
for(int i = 1; i <= n; ++i) fa[i] = i;
sort(edge.begin(), edge.end(), cmp); int N = edge.size() - 1;
for(int A, B, i = 0; i <= N; ++i){
A = find(edge[i].from); B = find(edge[i].to);
if(A == B) continue;
fa[A] = B; qwe.to = edge[i].to; qwe.dis = edge[i].dis;
sum += (long long)qwe.dis; edge[i].flag = true;
point[edge[i].from].push_back(qwe); qwe.to = edge[i].from;
point[edge[i].to].push_back(qwe);
}
}
void build(int t)
{
for(int i = point[t].size() - 1; i >= 0; --i){
int now = point[t][i].to;
if(now == node[t].fa) continue;
node[now].fa = t; node[now].dis = point[t][i].dis; node[now].deep = node[t].deep + 1;
build(now);
}
}
void prepare(int t)
{
node[t].tree[0][0] = node[t].fa; node[t].tree[0][1] = node[t].dis;
for(int i = 1; i <= 17; ++i){
if(pw[i] > node[t].deep) break;
node[t].tree[i][0] = node[node[t].tree[i - 1][0]].tree[i - 1][0];
// s.insert(node[node[t].tree[i - 1][0]].tree[i - 1][1]);
// s.insert(node[node[t].tree[i - 1][0]].tree[i - 1][2]);
// s.insert(node[t].tree[i - 1][1]);
// s.insert(node[t].tree[i - 1][2]);
// for(iter = s.begin(); iter != s.end(); ++iter){
// node[t].tree[i][2] = node[t].tree[i][1]; node[t].tree[i][1] = *iter;
// }
// s.clear();
tot = 0;
aaa[++tot] = node[node[t].tree[i - 1][0]].tree[i - 1][1];
aaa[++tot] = node[node[t].tree[i - 1][0]].tree[i - 1][2];
aaa[++tot] = node[t].tree[i - 1][1];
aaa[++tot] = node[t].tree[i - 1][2];
sort(aaa + 1, aaa + tot + 1); node[t].tree[i][1] = aaa[tot];
for(int k = tot - 1; k >= 1; --k){
if(aaa[k] != node[t].tree[i][1]){
node[t].tree[i][2] = aaa[k]; break;
}
}
}
for(int now, i = point[t].size() - 1; i >= 0; --i){
now = point[t][i].to;
if(now == node[t].fa) continue;
prepare(now);
}
}
inline void workk()
{
for(int A, B, lca, mx, i = edge.size() - 1; i >= 0; --i){
lin = edge[i]; A = lin.from; B = lin.to; mx = 0; tot = 0;
if(edge[i].flag) continue;
if(node[A].deep < node[B].deep) swap(A, B);
for(int k = 17; k >= 0; --k){
if(node[A].deep == node[B].deep) break;
if(node[node[A].tree[k][0]].deep >= node[B].deep && node[A].tree[k][0]){
//s.insert(node[A].tree[k][1]); s.insert(node[A].tree[k][2]);
aaa[++tot] = node[A].tree[k][1]; aaa[++tot] = node[A].tree[k][2];
A = node[A].tree[k][0];
}
}
if(A != B){
for(int k = 17; k >= 0; --k){
if(node[A].tree[k][0] != node[B].tree[k][0]){
// s.insert(node[A].tree[k][1]); s.insert(node[A].tree[k][2]);
// s.insert(node[B].tree[k][1]); s.insert(node[B].tree[k][2]);
aaa[++tot] = node[A].tree[k][1]; aaa[++tot] = node[A].tree[k][2];
aaa[++tot] = node[B].tree[k][1]; aaa[++tot] = node[B].tree[k][2];
A = node[A].tree[k][0]; B = node[B].tree[k][0];
}
}
aaa[++tot] = node[A].dis; aaa[++tot] = node[B].dis;
//s.insert(node[A].dis); s.insert(node[B].dis);
lca = node[A].fa;
}
if(A == B) lca = A;
// for(iter = s.begin(); iter != s.end(); ++iter){
// if(*iter != lin.dis) mx = max(mx, *iter);
// }
// s.clear();
sort(aaa + 1, aaa + 1 + tot);
for(int i = tot; i >= 1; --i){
if(aaa[i] != lin.dis){
mx = aaa[i]; break;
}
}
ans = min(ans, sum + lin.dis - mx);
}
}
int main()
{
putit();
kruskal();
build(root);
prepare(root);
workk();
cout << ans;
return 0;
}bzoj1977 [BeiJing2010组队]次小生成树 Tree
标签:class pac 基础 图片 TE read etc har +=
原文地址:https://www.cnblogs.com/LLppdd/p/9215637.html